yatbfm's blog
左神算法笔记
yatbfm
  2024-09-23 21:39   2025-01-22 11:27    17.5k 字  79 分钟  

1 时间复杂度和排序算法

1.1 交换两个数的写法

1
2
3
4
5
public void static swap(int[] arr, int i, int j) {
    arr[i] = arr[i] ^ arr[j];
    arr[j] = arr[i] ^ arr[j];
    arr[i] = arr[i] ^ arr[j];                                                           
}

异或操作：

  • 相同为0，不同为1
  • a ^ 0 = a

满足交换律和结合律。
对以上交换方法做解释：

  • 第一行：
    • arr[i] = arr[i] ^ arr[j];
    • arr[j] = arr[j];
  • 第二行：
    • arr[i] = arr[i] ^ arr[j];
    • arr[j] = arr[i] ^ arr[j] ^ arr[j] = arr[i];
  • 第三行
    • arr[i] = arr[i] ^ arr[j] ^ arr[j] = arr[i] ^ arr[j] ^ arr[i] = arr[j];
    • arr[j] = arr[i];

交换成功。
使用以上方法交换的前提是，两个变量指向的内存不能是同一片区域。
也就是说对数组进行交换时，交换的下标必须保证不相等。

1.2 找到数组中出现奇数次的数字

1.2.1 假设只有一种数出现奇数次

根据异或操作的结果，如果数字出现偶数次异或完之后会变成0，奇数次的还是原来本身，最后将0和奇数次的数异或还是它本身。

1
a ^ b ^ c ^ a ^ b ^ b ^ a ^ a ^ c = b;

因此只有一种数的可以直接遍历所有数然后异或，最终结果就是答案。

1.2.2 假设有两种数出现奇数次

首先根据异或操作结果，遍历一遍后，所有偶数次的数都会抵消，只剩下两个奇数次的数的异或记为eor = a ^ b，这里eor不为0，因为a和b是两种数，肯定不相等，所以eor肯定不是0，所以可以在eor中找到至少一个二进制位为1，假设这个二进制位为第i位，那么在第i位中，a和b的值一定不相同。
可以根据这个第i位的不同将所有数划分为第i位是1的和0的。

第i
位是0		 第i
位是1
others 0 others 1
a(或b) b(或a)

取另一个变量eorp遍历所有第i位是0或者1的，即可划分出a或者b。
这里可以知道eorp的值肯定为a或者b。因为others 0或者others 1一定是偶数个，最终会抵消。
因此最后将eor ^ eorp可以得到另一个奇数次的数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static void printOddTwiceNum(int[] arr) {
    int eor = 0;
    for (int cur : arr) {
        eor ^= cur;
    }
    int rightOne = eor & (~eor + 1);
    int eorp = 0;
    for (int cur : arr) {
        if ((cur & rightOne) == 0) {
            eorp ^= cur;
        }
    }
    // a = eorp, b = (eor ^ eorp)
}

上述代码中int rightOne = eor & (~eor + 1)，这行代码作用是获取到从右往左第一个不为0的位置上的数，并且让其他位都为0。其中~eor + 1是eor的补码。
假设eor = 10001010则~eor + 1 = 01110110异或后= 00000010。
需要注意的是if ((cur & rightOne) == 0)这里的条件只能是== 0 \ != 0 \ == rightOne \ != rightOne。因为rightOne其他位都是0，只有某一位是1，所以异或后的结果，只有这一位是0或者1。

1.3 插入排序

插入排序思想：假设0 - i位置的数有序，从i + 1位置向前看，将i + 1位置的数插入到前边有序的数组中使0 - i + 1的数仍然有序。将i + 1的数依次与前一个数比较，如果小于前一个数就交换，然后再与前一个数比较，直到不小于前一个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static void insertionSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    for (int i = 1; i < arr.length; i++) {
        for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
            swap(arr, j, j + 1);
        }
    }
}

public static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

这里的代码中将比较大小的条件放在了for循环中可以简化代码，同时要注意向前比较时下标不能越界。j指向的前一个数，j + 1指向当前的数，如果条件成立，即前一个数比当前的数大，就交换，交换后j--，然后下一次比较后j指向的仍然是前一个数，j + 1指向的仍然是当前的数。

1.4 Master公式

一个递归方法可以表示成如下的递推式：

当时，
当时，
当时，

1.5 归并排序

在数组中，每一个数的左边比当前数小的数累加起来，叫做这个数组的小和。例如[1, 3, 2, 4]，1左边没有比当前数小的；3左边有，是1；2左边有，是1；4左边有，是1 3 2，将这些所有加起来，即为小和。
解题思路可以利用归并排序，在合并过程中求小和。归并排序代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public static void mergeSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    mergeSort(arr, 0, arr.length - 1);
}

public static void mergeSort(int[] arr, int left, int right) {
    if (left >= right) {
        return;
    }
    // 新建临时数组
    int[] t = new int[right - left + 1];
    int mid = left + (right - left) / 2;
    // 对[left, mid]和[mid + 1, right]部分排序
    mergeSort(arr, left, mid);
    mergeSort(arr, mid + 1, right);
    // 将两个排序好的部分合并成一个部分
    int i = left, j = mid + 1, k = 0;
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            t[k++] = arr[i++];
        } else {
            t[k++] = arr[j++];
        }
    }
    // i和j只有一个满足
    while (i <= mid) {
        t[k++] = arr[i++];
    }
    while (j <= right) {
        t[k++] = arr[j++];
    }
    // 将排序好的部分修改回原始数组
    for (i = left, k = 0; i <= right; i++, k++) {
        arr[i] = t[k];
    }
}

同时需要转变一下思路，如果这个数的右边有比当前数大的数，那么当前数就会被加起来。
例如left = [1, 2, 2, 4]和right = [2, 3, 5]合并时，left[0] < right[0]，可以肯定，right数组中所有的数都比left[0]大，那么right这些数计算时都会加上left[0]，因此left[0]会被计算right.length - 0次。
而当合并到left[1] = right[0]时，和普通归并排序的合并过程略有不同，这里需要首先合并right数组，因为如果首先合并left数组，想要找到right数组中比left[1]大的数不太容易了，而首先合并right数组的话，可以让right的下标跳出相等的限制，当right的数比left[1]大，就可以找到有多少数比left[1]大，就可以求出小和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public int smallSum(int[] arr) {
    if (arr == null || arr.length < 2) {
        return -1;
    }
    return mergeSort(arr, 0, arr.length - 1);
}

private int mergeSort(int[] arr, int left, int right) {
    if (left >= right) {
        return 0;
    }
    int mid = left + (right - left) / 2;
    int ret = mergeSort(arr, left, mid) + mergeSort(arr, mid + 1, right);
    int i = left, j = mid + 1;
    int k = 0;
    int[] t = new int[right - left + 1];
    while (i <= mid && j <= right) {
        // 这里和归并排序过程不同
        if (arr[i] < arr[j]) {
            ret += arr[i] * (right - j + 1);
            t[k++] = arr[i++];
        } else {
            t[k++] = arr[j++];
        }
    }
    while (i <= mid) {
        t[k++] = arr[i++];
    }
    while (j <= right) {
        t[k++] = arr[j++];
    }
    for (i = left, k = 0; i <= right; i++, k++) {
        arr[i] = t[k];
    }
    return ret;
}

力扣逆序对问题。同样利用归并排序的过程，在归并过程中判断逆序对的数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public static int reversePairs(int[] arr) {
    if (arr == null || arr.length < 2) {
        return 0;
    }
    return reversePairs(arr, 0, arr.length - 1);
}

public static int reversePairs(int[] arr, int left, int right) {
    if (left >= right) {
        return 0;
    }
    int mid = left + (right - left) / 2;
    int ret = reversePairs(arr, left, mid) + reversePairs(arr, mid + 1, right);
    int[] t = new int[right - left + 1];
    int i = left, j = mid + 1, k = 0;
    while (i <= mid && j <= right) {
        // 如果arr[i] > arr[j]表明，i位置到mid位置的数都比j位置的数大，因为两个部分都是升序排序的。
        if (arr[i] <= arr[j]) {
            t[k++] = arr[i++];
        } else {
            t[k++] = arr[j++];
            ret += mid - i + 1;
        }
    }
    while (i <= mid) {
        t[k++] = arr[i++];
    }
    while (j <= right) {
        t[k++] = arr[j++];
    }
    for (i = left, k = 0; i <= right; i++, k++) {
        arr[i] = t[k];
    }
    return ret;
}

1.6 快速排序

这里采用三路排序，选取一个分界值x，然后划分出小于x的，等于x的，大于x的。然后分别对小于x的和大于x的排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public static void quickSort(int[] arr, int left, int right) {
    if (left >= right) {
        return;
    }
    // 随机选取一个分界值，可以有效减少最差情况
    int x = arr[left + (int) (Math.random() * (right - left + 1))];
    // 小于x的区间的最右端
    int less = left - 1;
    // less + 1到i - 1区间为等于x的区间，同时i会一直遍历待定的数据
    int i = left;
    // 大于x的区间的最左端
    int more = right + 1;
    while (i < more) {
        // 小于x，将i位置的数和小于x的区间的右端的数交换，并让区间向右扩，i加一，一步完成就是先右扩再交换。
        if (arr[i] < x) {
            swap(arr, i++, ++less);
        // 大于x，将i位置和大于x的区间的左端的数交换，然后让区间左扩，一步完成就是先左扩再交换。这里不让i加一是因为交换后，不知道交换过来的数是大于x等于x还是小于x，需要判断。
        } else if (arr[i] > x) {
            swap(arr, i, --more);
        // 等于x的，直接i加一。
        } else {
            i++;
        }
    }
    // 遍历一遍后，less及左边表示小于x的，more及右边表示大于x的
    quickSort(arr, left, less);
    quickSort(arr, more, right);
}

private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        quick_sort(nums, 0, nums.size() - 1);
        return nums;
    }
    // cpp 11随机数数引擎，需要引入random头文件。
    // 随机数范围：0到int最大值，每次启动程序调用生成的随机数序列相同，
    // 如果需要每次启动生成的不同可以设置当前时间为随机种子
    default_random_engine e;
    void quick_sort(vector<int> &arr, int left, int right) {
        if (left >= right) {
            return;
        }
        int x = arr[e() % (right - left + 1) + left];
        int less = left - 1, more = right + 1, i = left;
        while (i < more) {
            if (arr[i] < x) {
                swap(arr[++less], arr[i++]);
            } else if (arr[i] > x) {
                swap(arr[--more], arr[i]);
            } else {
                i++;
            }
        }
        quick_sort(arr, left, less);
        quick_sort(arr, more, right);
    }
};

1.7 堆

大根堆示例如下：

大根堆
每个根节点的值都要比孩子节点的值大，如果实行小根堆，则根节点的值要小于孩子节点的值。

以大根堆为例，主要实现两种操作：

  • 插入数据，在最后插入数据，然后依次向上操作，比较当前数和父节点的大小，如果大于父节点，则进行交换，然后父节点再和它的父节点比较。
    如下图，插入节点10，该系节点和父节点5比较，然后交换，最后和根节点9比较，然后交换。
1
  • 删除数据，如删除根节点的数据，可以将最后一个数覆盖掉根节点的数，然后向下操作。找到两个孩子（如果有）的最大值，和父节点进行比较，如果大于父节点，则交换，然后再从这个节点向下操作。
    基于上一个图，将根节点10删除后的状态应该是最后一个值5替换根节点，最后一个值5会被丢掉，这里用涂黑表示。然后从根节点索引0开始向下堆化操作。这里首先和最大的孩子节点9比较，然后交换。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// 向上操作，堆插入，其中index表示插入的值的索引。
public static void heapInsert(int[] arr, int index) {
    // 如果当前节点大于父节点，则进行交换，然后将索引更新为父节点索引。
    // 如果一直向上更新到根节点索引为0，0的父节点的索引计算完后还是0，堆插入终止
    while (arr[index] > arr[(index - 1) / 2]) {
        swap(arr, index, (index - 1) / 2);
        index = (index - 1) / 2;
    }
}
// 向下操作，堆化，其中index表示需要操作的索引，heapSize表示当前堆的大小。
public static void heapify(int[] arr, int index, int heapSize) {
    // 首先获取左孩子的索引
    int left = 2 * index + 1;
    // 如果有左孩子，这也表示有孩子。
    while (left < heapSize) {
        // left + 1表示右孩子，如果右孩子存在，并且值大于左孩子，两个孩子最大值的索引就是右孩子。
        // 如果右孩子不存在，或者右孩子值小于左孩子，那么最大值索引就是左孩子。
        int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
        // 比较孩子中的最大值和父节点，如果孩子值大于父节点的值，则赋值。
        largest = arr[largest] > arr[index] ? largest : index;
        // 如果最大值就是父节点自己本身，则说明满足大根堆，不操作。
        if (index == largest) {
            break;
        }
        swap(arr, index, largest);
        // 继续向下操作。
        index = largest;
        left = 2 * index + 1;
    }
}

public static void heapify(int[] arr, int index, int heapSize) {
    int t = index, left = 2 * index + 1, right = 2 * index + 2;
    if (left < heapSize && arr[left] > arr[t]) {
        t = left;
    }
    if (right < heapSize && arr[right] > arr[t]) {
        t = right;
    }
    if (t != index) {
        swap(arr, index, t);
        heapify(arr, t, heapSize);
    } 
}

如果要删除堆中的第一个元素也就是根节点，可以直接使用heapify方法，index设为0即可，但这个方法也支持从其他位置向下堆化操作。如果想要删除任意位置的元素：

  1. 将末尾的值覆盖掉要删除的元素的值。
  2. 基于当前位置进行向上或向下操作。
    1. 如果覆盖的值比原值大，则向上操作。
    2. 否则向下操作。

但是可以不必进行判断操作，因为在向上向下操作时，会首先判断是否满足条件，因此可以直接执行一次向上和向下操作即可。

堆的应用

1.8 堆排序扩展题

首先给前k+1个数放入小根堆中，那么小根堆的堆顶必然是所有的最小值。因为题目中说移动距离不超过k，那么最小值所在的位置最远是在索引k的位置。取出最小值放入数组，然后往后加入一个元素，选出第二个小的元素，依此类推。具体实现中可以手写堆，也可以使用优先队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static void sortedLessK(int[] arr, int k) {
    PriorityQueue<Integer> heap = new PriorityQueue<>();
    int index = 0;
    for (; index <= Math.min(arr.length, k); index++) {
        heap.add(arr[index]);
    }
    int i = 0;
    for (; index < arr.length; index++, i++) {
        arr[i] = heap.poll();
        heap.add(arr[index]);
    }
    while (!heap.isEmpty()) {
        arr[i++] = heap.poll();
    }
}

1.9 基数排序

待更新...

2 链表

2.1 回文链表的判断

回文链表

方法一

使用栈数据结构，遍历链表压栈，再依次出栈和原链表对比。
空间复杂度较高O(N)

方法二

快慢指针，快指针走到结尾时，慢指针走到中间，慢指针继续向下遍历，遍历过程反转后边的链表，最后从开始和结尾依次向中间遍历，比对。
空间复杂度O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public boolean isPalindrome(ListNode head) {
        if (head == null) {
            return true;
        }
        ListNode fast = head, slow = head;
        while (fast.next != null && fast.next.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        // 如果是奇数，快指针指向最后一个节点
        // 如果是偶数，快指针指向倒数第二个节点
        
        // slow再往下移动到右半部分的第一个节点。
        // 如果链表长度为偶数，移动后则正好在右半部分第一个；
        // 如果为奇数，那么可以认为中间的数不属于任何部分，他对整体的回文性没有影响，
        // 例如1 2 3 2 1，可以认为1 2 为左部分，2 1 为右部分，slow在右部分第一个节点2上
        slow = slow.next;
        // 保存反转后的链表头节点，为后续恢复链表做准备
        ListNode tempSlow = reverse(slow);
        fast = tempSlow;
        slow = head;
        while (fast != null) {
            if (slow.val != fast.val) {
                return false;
            }
            fast = fast.next;
            slow = slow.next;
        }
        // 恢复被反转的链表
        reverse(tempSlow);
        return true;
    }

    public ListNode reverse(ListNode head) {
        ListNode pre = null, cur = head;
        while (cur != null) {
            ListNode next = cur.next;
            cur.next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }
}

2.2 随机链表的复制

LCR 154. 复杂链表的复制 - 力扣（LeetCode）

方法一

使用哈希表，保存旧节点和新节点的键值对，然后遍历链表，将节点的下一个节点和随机节点复制。
空间复杂度O(N)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public Node copyRandomList(Node head) {
    if (head == null) {
        return null;
    }
    Map<Node, Node> hash = new HashMap<>();
    Node temp = head;
    while (temp != null) {
        Node copy = new Node(temp.val);
        hash.put(temp, copy);
        temp = temp.next;
    }
    temp = head;
    while (temp != null) {
        hash.get(temp).next = hash.get(temp.next);
        hash.get(temp).random = hash.get(temp.random);
        temp = temp.next;
    }
    return hash.get(head);
}

方法二

首先遍历链表，遍历过程中复制当前节点，然后将复制的节点加入到链表中的当前节点后，直到复制完所有节点。

复制完后，新复制的节点只有next指针有值，而random指针没有值，下一步在这个新链表上操作，将复制的节点的random连接到正确的节点上。因为每一个旧节点a的下一个一定是复制的节点a_copy，所以旧节点a的random指针指向的节点a_random的下一个节点a_random_copy（即复制的节点）就是a_copy的random指针应该指向的节点。如图蓝色的箭头即为复制的节点的random指针的正确指向。
实际中需要注意：random指针可能指向null，此时需要进行判空操作。

最后遍历链表，将新复制的链表拆分出来，然后组成新的链表即可，同时原链表也要恢复原状。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/
class Solution {
    public Node copyRandomList(Node head) {
        if (head == null) {
            return null;
        }
        Node temp = head;
        while (temp != null) {
            Node copy = new Node(temp.val);
            copy.next = temp.next;
            temp.next = copy;
            temp = temp.next.next;
        }
        temp = head;
        while (temp != null) {
            Node copy = temp.next;
            copy.random = temp.random == null ? null : temp.random.next;
            temp = temp.next.next;
        }
        temp = head;
        Node headcopy = head.next;
        while (temp != null) {
            Node copy = temp.next;
            temp.next = copy.next;
            temp = temp.next;
            copy.next = temp == null ? null : temp.next;
        }
        return headcopy;
    }
}

2.3 判断一个链表是否有环，以及返回入环节点

环形链表I
环形链表II

方法一

使用哈希表，遍历整个链表，依次存入链表，存入之前判断是否已经存在，如果存在则当前链表为入环的第一个节点。

1
2
3
4
5
6
7
8
9
10
11
12
public ListNode detectCycle(ListNode head) {
    if (head == null) {
        return null;
    }
    Set<ListNode> set = new HashSet<>();
    ListNode temp = head;
    while (temp != null && !set.contains(temp)) {
        set.add(temp);
        temp = temp.next;
    }
    return temp;
}

方法二

快慢指针，快指针一次走两步，慢指针一次走一步，如果快指针遇到null则无环，否则当快慢指针相遇时有环，此时让快指针从头节点开始一次一步，慢指针一次一步，当快慢指针再次相遇时，该节点为入环的第一个节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null) {
            return false;
        }
        ListNode fast = head, slow = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (fast == slow) {
                return true;
            }
        }
        return false;
    }
    // pos表示fast和slow相遇的位置
    public ListNode first(ListNode head, ListNode pos) {
        while (head != pos) {
            head = head.next;
            pos = pos.next;
        }
        return head;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
if (head == null) {
    return null;
}
ListNode fast = head, slow = head;
while (fast.next != null && fast.next.next != null) {
    slow = slow.next;
    fast = fast.next.next;
    // 当快慢指针相同时，必然有环，因此使fast指针为头指针，快慢指针同时移动，即可找到入环节点
    if (fast == slow) {
        fast = head;
        while (fast != slow) {
            slow = slow.next;
            fast = fast.next;
        }
        return slow;
    }
}
// 走到这一步说明快慢指针不相等，并且快指针可以走到头，那说明没环
return null;

2.4 判断两个链表是否相交

这里认为链表都是单链表

  1. 情况1：两个链表都无环
    双指针，遍历链表A和B，当指针为null时从另一个节点的头节点开始遍历。直到两个指针相等（两个指针相等时，如果为null则表示没有相交节点，否则有相交节点）
    面试题 02.07. 链表相交 - 力扣（LeetCode）
1
2
3
4
5
6
7
8
9
10
11
12
13
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) {
            return null;
        }
        ListNode pA = headA, pB = headB;
        while (pA != pB) {
            pA = pA == null ? headB : pA.next;
            pB = pB == null ? headA : pB.next;
        }
        return pA;
    }
}

❗注意：判断是否为null时，使用的是pA当前指针，而不是pA.next，如果使用pA.next来判断，当不相交时，会发生无限循环的情况，pA和pB会一直不相等（也不为null)。所以使用pA当前指针。可以理解为，把最后链表结束时指向的null指针也算作一个节点，然后两个链表不相交时，最后都会指向null节点，那么两个链表就在null节点“相交”了，如下图所示。

  1. 情况2：一个有环一个无环（一定不相交）
    如果相交，则肯定有一个节点有两个next指针，这不满足单链表。所以一定不相交。
  2. 情况3：两个都有环
  3. 不相交
  4. 在非环处相交
  5. 在环处相交

相交只有两种情况

找到两个带环链表的入环节点，然后固定一个，遍历另一个，直到能找到一个节点和固定节点相等，则证明相交，否则不相交。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// circleNode1 circleNode2是两个节点的入环节点

// 如果入环节点相同，说明必然是情况1。否则是情况2或者不相交
if (circleNode1 == circleNode2) {
    // 利用circleNode1或者2为末尾节点，利用无环链表求相交节点方式求相交的节点。
    return true;
}
Node temp = circleNode2.next;
while(temp != circleNode2) {
    if(temp == circleNode1)
        // circleNode1 或者  circleNode2为相交节点都可以
        return true;
    temp = temp.next;
}
// 不相交
return false;

所以所有情况如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public static ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    ListNode cycleNodeA = hasCycle(headA);
    ListNode cycleNodeB = hasCycle(headB);
    if (cycleNodeA == cycleNodeB) {
        // 说明两个都是无环的，直接判断是否相交
        // if (cycleNodeA == null) {
        //     return getIntersectionNodeNoLoop(headA, headB, null);
        // }
        // 否则是都有环，入环节点相同，必然相交，以入环节点为终止节点求相交节点
        // return getIntersectionNodeNoLoop(headA, headB, cycleNodeA);
        // 以上代码可以直接合并为下面一行
        return getIntersectionNodeNoLoop(headA, headB, cycleNodeA);
    }
    // 说明两个入环节点不相等，要么有一个为空，要么都不为空，如果有一个为空，则表示肯定不相交
    if (cycleNodeA == null || cycleNodeB == null) {
        return null;
    }
    // 如果环上相交，说明从一个入环节点开始遍历，一定能到达另一个入环节点
    ListNode temp = cycleNodeA;
    while (temp != cycleNodeB) {
        temp = temp.next;
        // 转了一圈发现回到原位置了，说明没有相交
        if (temp == cycleNodeA) {
            return null;
        }
    }
    // 相交，任意一个入环节点都可以是相交节点。
    return cycleNodeA;
    // 如果入环节点不同，并且相交，那么肯定有两个相交节点
    // return cycleNodeB;
}
// 判断一个链表是否有环
public static ListNode hasCycle(ListNode head) {
    if (head == null) {
        return null;
    }
    ListNode slow = head, fast = head;
    while (fast.next != null && fast.next.next != null) {
        slow = slow.next;
        fast = fast.next.next;
        if (fast == slow) {
            fast = head;
            while (fast != slow) {
                fast = fast.next;
                slow = slow.next;
            }
            return fast;
        }
    }
    return null;
}
// 判断两个无环链表是否相交，手动设定终止节点endNode
public static ListNode getIntersectionNodeNoLoop(ListNode headA, ListNode headB, ListNode endNode) {
    ListNode pA = headA, pB = headB;
    while (pA != pB) {
        pA = pA == endNode ? headB : pA.next;
        pB = pB == endNode ? headA : pB.next;
    }
    return pA;
}

2.5 找到两个有序链表相同的节点


解题思路：因为两个链表都是有序的，采用双指针。比较当前值，较小的指针向后移动，如果相等了，加入结果集，同时向后移动，然后继续比较，直到一个越界。

2.6 把链表按某个值分为小于 等于 大于的部分

排序链表

入门做法

把链表每个节点(不是值，是节点Node)放在数组里，然后使用快排中的partition。

高级做法

首先准备6个指针，分别表示：

smallHead 小于部分的头指针
smallTail 小于部分的尾指针
equalHead 等于部分的头指针
equalTail 等于部分的尾指针
bigHead 大于部分的头指针
bigTail 大于部分的尾指针

使用这六个指针分别串联出小于部分、等于部分、大于部分的链表。
遍历整个链表，如果遇到小于的节点，加入到小于部分的链表中，也就是利用尾插法插入到以smallHead为头结点的链表的末尾，等于、大于的节点同理。
最后将小于部分的尾连接到等于部分的头，等于部分的尾连接到大于部分的头。
但是在实现时要注意：可能不存在小于部分或者等于部分等等，要对每个进行判空处理，防止出现空指针异常。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public static ListNode listPartition(ListNode head, int pivot) {
    // 构造三个类分别表示小于部分的链表，等于部分、大于部分的链表
    PartitionNode small = new PartitionNode();
    PartitionNode equal = new PartitionNode();
    PartitionNode big = new PartitionNode();
    ListNode temp = head;
    while (temp != null) {
        // 需要频繁插入节点到尾节点，因此用一个方法包装，减少代码量。
        if (temp.val < pivot) {
            small.insertTail(temp);
        } else if (temp.val > pivot) {
            big.insertTail(temp);
        } else {
            equal.insertTail(temp);
        }
        temp = temp.next;
    }
    // 最终需要判断小于部分和等于部分的空值情况。
    // 如果小于部分不为空，然后等于部分不为空，则连接到等于部分，再连接到大于部分，如果等于部分为空，则直接连接到大于部分
    // 如果小于部分为空，等于部分不为空，则连接到大于部分，如果等于部分为空，则说明只有大于部分，直接返回大于部分
    if (small.head != null) {
        if (equal.head != null) {
            small.tail.next = equal.head;
            equal.tail.next = big.head;
        } else {
            small.tail.next = big.head;
        }
        return small.head;
    } else if (equal.head != null) {
        equal.tail.next = big.head;
        return equal.head;
    }
    return big.head;
}
// 定义一个类包含头节点和尾节点。
// 算法实现时会频繁在尾部插入节点，会改变头尾指针的值，因此在类中定义头尾指针。
static class PartitionNode {
    ListNode head, tail;

    void insertTail(ListNode node) {
        if (head == null) {
            head = tail = node;
        } else {
            tail.next = node;
            tail = node;
        }
    }
}
// 定义节点类
static class ListNode {
    int val;
    ListNode next;

    public ListNode(int val) {
        this.val = val;
        this.next = null;
    }
}

链表快速排序

由此引出对链表的快速排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
public static PartitionNode quickSortList(ListNode head) {
    if (head == null || head.next == null) {
        return new PartitionNode(head, head);
    }

    // 通过快慢指针找到中间位置的节点作为中间值，防止边缘特殊情况使算法退化
    ListNode pivotNode;
    ListNode slow = head, fast = head;
    while (fast.next != null && fast.next.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    pivotNode = slow;
    // 划分成三部分。
    PartitionNode small = new PartitionNode();
    PartitionNode equal = new PartitionNode();
    PartitionNode big = new PartitionNode();
    ListNode temp = head;
    while (temp != null) {
        if (temp.val < pivotNode.val) {
            small.insertTail(temp);
        } else if (temp.val > pivotNode.val) {
            big.insertTail(temp);
        } else {
            equal.insertTail(temp);
        }
        temp = temp.next;
    }
    // 划分后对每部分的链表尾节点添加null值，使这三部分链表独立。
    if (small.head != null) {
        small.tail.next = null;
    }
    if (equal.head != null) {
        equal.tail.next = null;
    }
    if (big.head != null) {
        big.tail.next = null;
    }
    // 递归排序每部分链表
    small = quickSortList(small.head);
    big = quickSortList(big.head);
    // 连接三部分链表。
    if (small.head != null) {
        if (equal.head != null) {
            small.tail.next = equal.head;
            // 该算法中返回的是完整的链表头节点和尾节点，所以需要确保返回的small的tail对象为整个链表的尾节点
            // 后续该操作同理，否则会导致数据丢失。
            small.tail = equal.tail;
            equal.tail.next = big.head;
        } else {
            small.tail.next = big.head;
        }
        small.tail = big.tail == null ? small.tail : big.tail;
        return small;
    } else if (equal.head != null) {
        equal.tail.next = big.head;
        equal.tail = big.tail == null ? equal.tail : big.tail;
        return equal;
    }
    return big;
}
    
class PartitionNode {
    ListNode head, tail;
    
    void insertTail(ListNode node) {
        if (head == null) {
            head = tail = node;
        } else {
            tail.next = node;
            tail = node;
        }
    }
    
    public PartitionNode() {
    }
    
    public PartitionNode(ListNode head, ListNode tail) {
        this.head = head;
        this.tail = tail;
    }
}
    
class ListNode {
    int val;
    ListNode next;
    
    public ListNode(int val) {
        this.val = val;
        this.next = null;
    }
}

链表归并排序

对于链表的排序，使用归并排序是更好的选择，可以采用更少的代码完成，同时可以使用迭代的方式优化排序，使空间复杂度O(logn)优化为O(1)。
这里先使用递归形式的归并排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public static ListNode mergeSort(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }
    // 使用快慢指针找到中点，如果是奇数个，中点是正中间，如果是偶数，中点是中间两个数的左边的
    ListNode fast = head, slow = head;
    while (fast.next != null && fast.next.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    // 保存慢指针向后移动一个的指针，作为右半部分的起点
    // 同时让慢指针的next指向null，表示左半部分和右半部分分成了两个链表。
    ListNode mid = slow.next;
    slow.next = null;
    // 拆分
    ListNode left = mergeSort(head);
    ListNode right = mergeSort(mid);
    // 左右分别排序后，进行归并，这里使用尾插法，保证稳定性。
    ListNode ret = new ListNode(0);
    ListNode tail = ret;
    while (left != null && right != null) {
        if (left.val <= right.val) {
            tail.next = left;
            left = left.next;
        } else {
            tail.next = right;
            right = right.next;
        }
        tail = tail.next;
    }
    // 有一个链表没遍历完，放到最后即可。
    tail.next = left == null ? right : left;
    return ret.next;
}

❗空间复杂度O(1)的待更新

3 二叉树

3.1 遍历

递归、非递归的前中后序遍历要会写。

3.1.1 前中后序遍历（非递归）

  1. 前序遍历

首先设置一个栈结构用于存储。整体遍历流程如下：
❗上述过程要注意：加入孩子节点时一定是先加入右孩子，再加入左孩子，因为栈是后进先出的顺序，所以要后加入左孩子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static void preOrderUnRecur(Tree root) {
    if (root == null) {
        return;
    }
    Stack<Tree> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        Tree pop = stack.pop();
        System.out.print(pop.val + " ");
        if (pop.right != null) {
            stack.push(pop.right);
        }
        if (pop.left != null) {
            stack.push(pop.left);
        }
    }
    System.out.println();
}
  1. 后序遍历

前序遍历的顺序是：根左右，后序遍历的顺序是：左右根。假设现在有前序'（前序撇）遍历：根右左，那么将这个前序'遍历的顺序加入到另一个栈中，最后统一输出，根据栈的现先进后出顺序，那么输出的结果是：左右根。这就是后序遍历的做法。
❗有一点注意：前序遍历时保证根左右的顺序，加入子孩子时先加入的右孩子，而现在需要根据前序遍历得到前序'遍历即根右左的顺序，因此需要先加入左孩子。
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public static void postOrderUnRecur(Tree root) {
    if (root == null) {
        return;
    }
    Stack<Tree> stack1 = new Stack<>();
    // 该栈用于收集结果，最后统一将节点输出，满足后序遍历结果
    Stack<Tree> stack2 = new Stack<>();
    stack1.push(root);
    while (!stack1.isEmpty()) {
        Tree pop = stack1.pop();
        // 暂时不打印，首先加入到结果栈中
        stack2.push(pop);
        // 先加入左孩子，保证在加入结果栈时可以先出
        if (pop.left != null) {
            stack1.push(pop.left);
        }
        if (pop.right != null) {
            stack1.push(pop.right);
        }
    }
    // 统一输出
    while (!stack2.isEmpty()) {
        System.out.print(stack2.pop().val + " ");
    }
    System.out.println();
}
  1. 中序遍历

中序遍历顺序：左根右。算法流程：

  1. 如果左孩子不为空，压栈，将新压入的节点设置为“当前节点”继续执行a
  2. 如果左孩子为空，弹出栈，打印
  3. 将弹出栈的节点的右孩子设置为“当前节点”，继续执行a
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public static void midOrderUnRecur(Tree root) {
    if (root == null) {
        return;
    }
    Stack<Tree> stack = new Stack<>();
    // 设置一个指针指向当前遍历到哪个节点，也可以复用root指针
    Tree temp = root;
    // temp != null这个条件是必要的
    while (!stack.isEmpty() || temp != null) {
        // 如果当前指针不为null，压栈
        while (temp != null) {
            stack.push(temp);
            // 将当前指针指向左孩子
            temp = temp.left;
        }
        // 说明左孩子为空了，出栈
        temp = stack.pop();
        // 打印
        System.out.print(temp.val + " ");
        // 将当前指针指向右孩子，重复上述操作
        temp = temp.right;
    }
    System.out.println();
}

❗中序遍历和前边的前序后序遍历代码区别较大，增加了一个指针指向当前遍历到了哪个节点，而且while循环条件中的temp != null是必需的，因为当栈空的时候，指针可能指向了根节点的右孩子，此时还没有遍历完，需要这个条件，防止丢失数据。

3.1.2 层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static void levelOrder(Tree root) {
    if (root == null) {
        return;
    }
    Queue<Tree> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        Tree remove = queue.remove();
        System.out.print(remove.val + " ");
        if (remove.left != null) {
            queue.add(remove.left);
        }
        if (remove.right != null) {
            queue.add(remove.right);
        }
    }
    System.out.println();
}

3.2 求二叉树一层最多的节点个数（每一层的节点个数）

LeetCode 102
使用一个变量保存当前层的个数，然后一次性弹出当前层所有的节点，同时加入所有下一层的节点，这样可以保证每次弹出的节点都是同一层的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public static int getMaxLevelNodes(Tree root) {
    Queue<Tree> queue = new LinkedList<>();
    queue.add(root);
    int maxCnt = 0;
    while (!queue.isEmpty()) {
        // size即为当前层的节点个数
        int size = queue.size();
        maxCnt = Math.max(maxCnt, size);
        // 一次弹出完该层所有的节点
        for (int i = 0; i < size; i++) {
            Tree remove = queue.remove();
            if (remove.left != null) {
                queue.add(remove.left);
            }
            if (remove.right != null) {
                queue.add(remove.right);
            }
        }
    }
    return maxCnt;
}

3.3 二叉树的最大宽度

二叉树最大宽度
这道题需要加上两个非空节点中间的null节点的数量，可以按照完全二叉树对数进行编号，然后使用最右端的非空节点索引减去最左端非空节点的索引+1即可得到这一层的宽度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// 自定义实现Pair类，用于存储节点和对应的索引值
static class Pair<T, V> {
    T key;
    V value;

    public Pair(T key, V value) {
        this.key = key;
        this.value = value;
    }
}
public static int widthOfBinaryTree(Tree root) {
    if (root == null) {
        return 0;
    }
    Queue<Pair<Tree, Integer>> queue = new LinkedList<>();
    // 存储根节点和索引
    queue.add(new Pair<>(root, 0));
    int maxCnt = 0;
    while (!queue.isEmpty()) {
        // 按照求每层节点个数的方法
        int size = queue.size();
        // 记录每层节点的最小索引和最大索引
        int minIndex = Integer.MAX_VALUE, maxIndex = Integer.MIN_VALUE;
        for (int i = 0; i < size; i++) {
            Pair<Tree, Integer> pair = queue.remove();
            Tree node = pair.key;
            Integer index = pair.value;
            minIndex = Math.min(minIndex, index);
            maxIndex = Math.max(maxIndex, index);
            // 左孩子索引为当前索引 * 2 + 1
            if (node.left != null) {
                queue.add(new Pair<>(node.left, 2 * index + 1));
            }
            // 右孩子索引为当前索引 * 2 + 2
            if (node.right != null) {
                queue.add(new Pair<>(node.right, 2 * index + 2));
            }
        }
        maxCnt = Math.max(maxCnt, maxIndex - minIndex + 1);
    }
    return maxCnt;
}

3.4 判断是否是完全二叉树

LeetCode 958
方法1：分两种情况：

  1. 对于任一个节点，如果有右孩子但无左孩子，直接返回false
  2. 在条件1不违反的条件下，如果遇到了第一个左右孩子不全的，如只有左孩子或者没有孩子，那么之后的节点必须全部是叶节点。

☆方法2：层序遍历时将为null的节点也加入进去，如果出现null后，后续出现的节点都要是null否则就不是完全二叉树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public boolean isCompleteTree(TreeNode root) {
    if (root == null) {
        return true;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    // 设置标记为表示是否出现了null节点
    boolean flag = false;
    while (!queue.isEmpty()) {
        TreeNode node = queue.remove();
        if (node == null) {
            flag = true;
        } else {
            // 如果node不为null,但是flag为true,说明之前出现过null节点,就不是完全二叉树了
            if (flag) {
                return false;
            }
            queue.add(node.left);
            queue.add(node.right);
        }
    }
    return true;
}

3.5 判断满二叉树

满二叉树的特征：

  • 每一层的节点个数=从开始
  • 按照完全二叉树的索引编号，最后一个节点的编号为：从开始

本题从每一层节点个数判断，从3.2 求二叉树一层最多的节点个数复用代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static boolean isFullBiTree(Tree root) {
    if (root == null) {
        return true;
    }
    // 记录高度
    int height = 0;
    Queue<Tree> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        int size = queue.size();
        // 判断当前层节点个数是否满足条件
        if (size != Math.pow(2, height)) {
            return false;
        }
        for (int i = 0; i < size; i++) {
            Tree node = queue.remove();
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
        }
        height++;
    }
    return true;
}

3.6 判断平衡二叉树

LeetCode 110
通过求两个子树的高度过程中判断是否是平衡的。
类似于后序遍历。如果子树都不是平衡的，那么整棵树一定不是平衡的。通过设立标志位返回值判断是否是平衡的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public boolean isBalanced(TreeNode root) {
        return getHeight(root) >= 0;
    }

    public int getHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        // 如果高度返回-1，说明子树已经是不平衡的了，那么该棵树也是不平衡的。
        // 如果高度都不是-1，说明子树平衡，然后判断整棵树，如果整棵树也不平衡那么返回-1
        if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {
            return -1;
        }
        return Math.max(leftHeight, rightHeight) + 1;
    }
}

3.7 判断是否是二叉搜索树

LeetCode 98
利用二叉搜索树的定义，中序遍历时判断上一个数是否小于当前的数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 存储中序遍历的上一个遍历到的值,使用Long类型最小值,Integer类型最小值会越界
private long pre = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
    if (root == null) {
        return true;
    }
    // 如果左数不满足条件,整棵树肯定不满足,直接退出
    boolean left = isValidBST(root.left);
    if (!left) {
        return false;
    }
    // 如果上一个数不小于当前的,说明也不满足
    if (pre >= root.val) {
        return false;
    }
    // 重置pre,方便下次使用
    pre = root.val;
    // 判断右树
    return isValidBST(root.right);
}

3.8 找到二叉树两个节点的最低公共祖先节点

LeetCode 236
236. 二叉树的最近公共祖先 - 力扣（LeetCode）题解
遍历节点，当前节点如果为null或者p``q直接返回。否则遍历左右子树。分别获取到左右子树的返回值。

  • 如果左子树返回空，说明左子树肯定不存在p``q，直接返回right因为必然存在在right中。
  • 如果左子树返回不空右子树返回空，则说明肯定存在在左子树中，返回left。
  • 如果都不空，说明左右子树都存在分别存在p``q，则当前root为公共祖先，返回当前的root为公共祖先。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (root == null || root == p || root == q) {
        return root;
    }
    TreeNode left = lowestCommonAncestor(root.left, p, q);
    TreeNode right = lowestCommonAncestor(root.right, p, q);
    if (left == null) {
        return right;
    }
    if (right == null) {
        return left;
    }
    return root;
}

3.9 二叉搜索树的中序后继

LeetCode 053
视频讲解：6. 图_哔哩哔哩_bilibili（二叉树的中序后继），二叉搜索树可看作是特殊情况
首先根据中序遍历的顺序：左根右，一个节点的后续节点是右子树的最左端的节点。
所以如果要查找的节点有右子树，那么直接遍历到右子树的最左端节点，即为后续节点。
如果没有右子树，那么后续节点一定在该节点的祖先节点上。因为以当前节点为根的子树没有右子树，说明当前节点子树遍历完了，后续节点一定在某个祖先节点或者没有后续节点。

如上图，第一种情况的后续节点是e，第二种后续节点是b，第三种后续节点是a。针对情况2和3即待查找节点p没有右子树的情况下：

  • 如果p在根节点的左子树中，那么根节点可能就是p的后续节点，后续节点也可能是根节点的左子树中。
  • 如果p在根节点的右子树中，那么根节点就不是p的后续节点

那么怎么判断p在根节点的左子树还是右子树呢？这就用到了二叉搜索树的性质，如果p节点的值比根节点小那么p就在根节点左子树中，否则在右子树。
所以算法如下：

  • 首先判断有没有右子树，如果有则直接找到右子树最左端节点返回。如果没有则执行下边操作
  • 从根节点开始遍历，依次和p比较，判断p在根节点的哪个子树中
    • 如果在左子树中，更新保存答案的变量，继续左子树
    • 如果在右子树中，不更新，直接遍历右子树
    • 直接遍历到最后为null
  • 返回结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
    if (root == null) {
        return null;
    }
    if (p.right != null) {
        TreeNode temp = p.right;
        while (temp.left != null) {
            temp = temp.left;
        }
        return temp;
    }
    TreeNode temp = root;
    TreeNode ret = null;
    while (temp != null) {
        // 如果p的值大于等于当前根节点的值，说明p在右子树中，当前节点肯定不会是后续节点，所以直接遍历右子树
        // 如果p的值小于当前根节点的值，说明p在左子树中，根据中序遍历顺序：左根右，当前根节点可能是后续节点，
        // 因此先保存当前节点为答案，然后继续遍历左子树（左子树中可能存在真正的后续节点）
        if (temp.val <= p.val) {
            temp = temp.right;
        } else {
            ret = temp;
            temp = temp.left;
        }
    }
    return ret;
}

3.10 二叉树的序列化与反序列化

B站视频

3.11 判断是否是二叉树

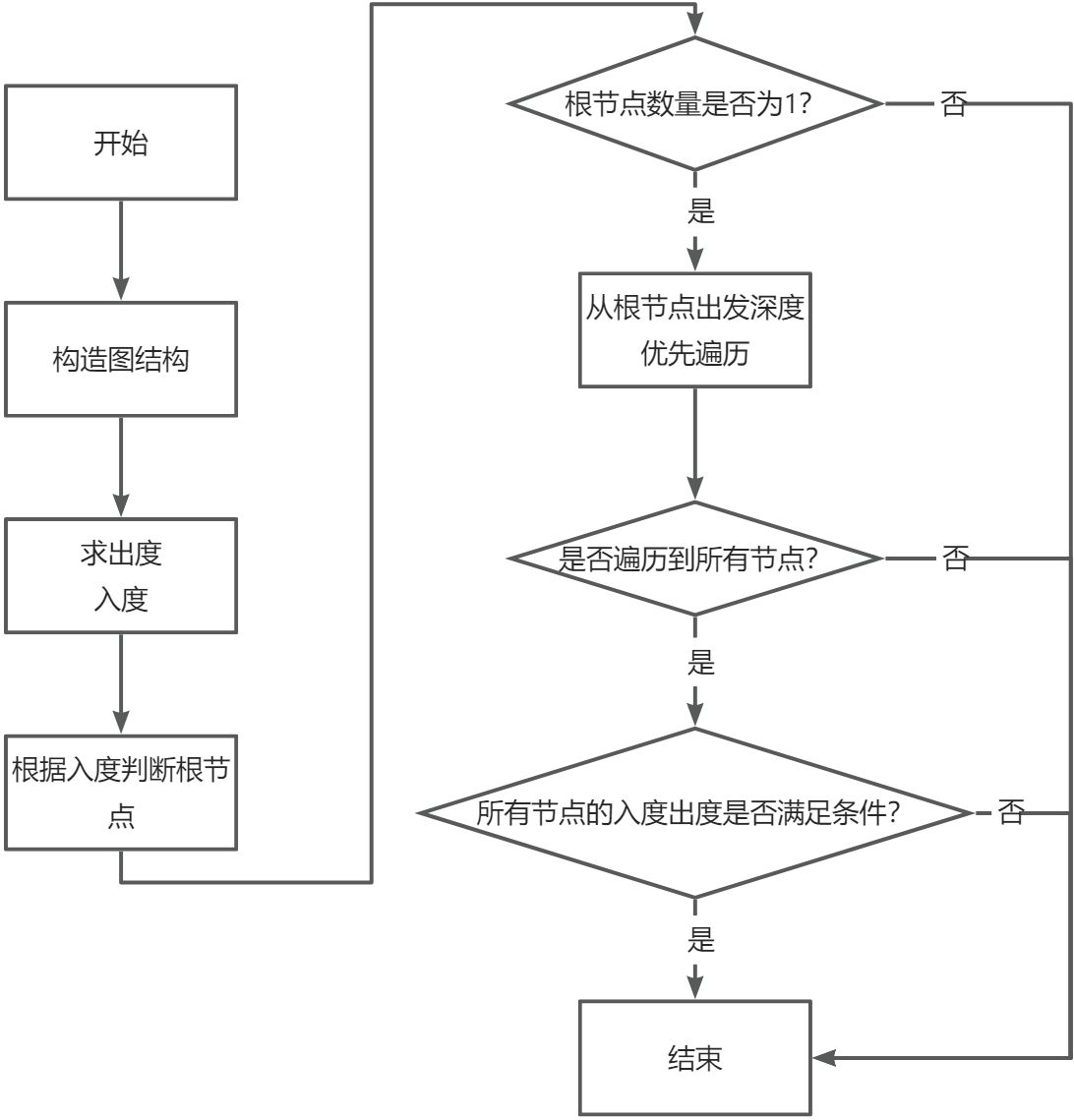
给定n个节点和m条有向边，节点从[0, n - 1]表示，m条边使用(a, b)的数对（a指向b）表示为b的父节点是a。判断给定的结果是不是二叉树。
🍬思路：
将二叉树看成是一个有向图，除根节点外每个节点的入度为1、出度小于等于2，根节点的入度必须为0、出度小于等于2且只有一个根节点，同时保证从根节点出发可以遍历到所有的节点。
可能存在的图的情况：

  1. 正确
  2. 出度不满足条件
  3. 入度不满足条件

树中存在父子节点之间“互为父子”，则可以从出入度判断不满足条件 4. 根节点个数不满足条件

根节点个数大于1 根节点个数为0 5. 从根节点遍历不能遍历到所有节点

从出入度判断，只有一个入度为0的节点，所以无法从入度为0的个数判断图是否连通，需要使用dfs遍历 因此根据上述条件总结出算法流程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
void dfs(vector<vector<int>> &g, int t, bool *st) {
    st[t] = true;
    for (int i = 0; i < g[t].size(); i++) {
        if (!st[g[t][i]]) {
            dfs(g, g[t][i], st);
        }
    }
}
// 判断是否是二叉树
bool isBinaryTree(int n, vector<pair<int, int>> &edges) {
    // 构造图
    vector<vector<int>> g(n, vector<int>());
    for (int i = 0; i < edges.size(); i++) {
        g[edges[i].first].push_back(edges[i].second);
    }
    // 求出入度
    int inDegree[n], outDegree[n];
    for (int i = 0; i < n; i++) {
        inDegree[i] = 0;
        outDegree[i] = 0;
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < g[i].size(); j++) {
            outDegree[i]++;
            inDegree[g[i][j]]++;
        }
    }
    // 判断根节点数量和索引
    int rootIndex = -1, rootCnt = 0;
    for (int i = 0; i < n; i++) {
        if (inDegree[i] == 0) {
            rootCnt++;
            rootIndex = i;
        }
    }
    if (rootCnt != 1) {
        return false;
    }
    // 从根节点遍历是否能遍历到所有节点
    bool st[n];
    for (int i = 0; i < n; i++) {
        st[i] = false;
    }
    dfs(g, rootIndex, st);
    for (int i = 0; i < n; i++) {
        if (!st[i]) {
            return false;
        }
    }
    // 判断出入度是否满足条件
    for (int i = 0; i < n; i++) {
        if (outDegree[i] > 2) {
            return false;
        }
        if (i == rootIndex) {
            continue;
        }
        if (inDegree[i] != 1) {
            return false;
        }
    }
    return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public class Solution {
    public boolean isBinaryTree(int n, List<Integer[]> edges) {
        List<List<Integer>> g = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            g.add(new ArrayList<>());
        }
        for (Integer[] e : edges) {
            g.get(e[0]).add(e[1]);
        }
        int[] inDegree = new int[n];
        int[] outDegree = new int[n];
        Arrays.fill(inDegree, 0);
        Arrays.fill(outDegree, 0);
        for (int i = 0; i < n; i++) {
            for (int j : g.get(i)) {
                outDegree[i]++;
                inDegree[j]++;
            }
        }
        int rootIndex = -1, rootCnt = 0;
        for (int i = 0; i < n; i++) {
            if (inDegree[i] == 0) {
                rootCnt++;
                rootIndex = i;
            }
        }
        if (rootCnt != 1) {
            return false;
        }
        boolean[] st = new boolean[n];
        dfs(g, rootIndex, st);
        for (int i = 0; i < n; i++) {
            if (!st[i]) {
                return false;
            }
        }
        for (int i = 0; i < n; i++) {
            if (outDegree[i] > 2) {
                return false;
            }
            if (i == rootIndex) {
                continue;
            }
            if (inDegree[i] != 1) {
                return false;
            }
        }

        return true;
    }

    private void dfs(List<List<Integer>> g, int t, boolean[] st) {
        st[t] = true;
        for (int j : g.get(t)) {
            if (!st[j]) {
                dfs(g, j, st);
            }
        }
    }
}

4 图

4.1 图的存储

这种方式，对于很多算法都很方便，难点在于给定一个图结构，首先需要把给定的图结构转换成该图结构。对于某些算法用不到某些数据，如 入度in和出度out可以不写

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
public class Graph {
    // 如果知道确切的顶点个数，可以使用数组代替HashMap
	public HashMap<Integer, Node> nodes;
	public HashSet<Edge> edges;
	
	public Graph() {
		nodes = new HashMap<>();
		edges = new HashSet<>();
	}
}

// 点结构的描述
public class Node {
	public int value;
	public int in;
	public int out;
	public ArrayList<Node> nexts;
	public ArrayList<Edge> edges;

	public Node(int value) {
		this.value = value;
		in = 0;
		out = 0;
		nexts = new ArrayList<>();
		edges = new ArrayList<>();
	}
}

public class Edge {
	public int weight;
	public Node from;
	public Node to;

	public Edge(int weight, Node from, Node to) {
		this.weight = weight;
		this.from = from;
		this.to = to;
	}

}

// matrix 所有的边
// N*3 的矩阵
// [weight, from节点上面的值，to节点上面的值]
// 
// [ 5 , 0 , 7]
// [ 3 , 0,  1]
// 
public static Graph createGraph(int[][] matrix) {
	Graph graph = new Graph();
	for (int i = 0; i < matrix.length; i++) {
		 // 拿到每一条边， matrix[i] 
		int weight = matrix[i][0];
		int from = matrix[i][1];
		int to = matrix[i][2];
        graph.nodes.putIfAbsent(from, new Node(from));
		// if (!graph.nodes.containsKey(from)) {
		// 	graph.nodes.put(from, new Node(from));
		// }
        graph.nodes.putIfAbsent(to, new Node(to));
		// if (!graph.nodes.containsKey(to)) {
		// 	graph.nodes.put(to, new Node(to));
		// }
		Node fromNode = graph.nodes.get(from);
		Node toNode = graph.nodes.get(to);
		// 无向图可以看作是两条边的有向图
        // 第一条边
        Edge edge = new Edge(weight, fromNode, toNode);
        fromNode.nextNodes.add(toNode);
        fromNode.edges.add(edge);
        fromNode.out++;
        toNode.in++;
        graph.edges.add(edge);
        // 第二条边
        edge = new Edge(weight, toNode, fromNode);
        toNode.nextNodes.add(fromNode);
        toNode.edges.add(edge);
        toNode.out++;
        fromNode.in++;
        graph.edges.add(edge);
	}
	return graph;
}

这个版本代码量少，易于理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 存储每个顶点的信息和该顶点所有边的信息。
class Node {
    public List<Edge> edges = new ArrayList<>();
}
// 存储每条边的信息（也可以用链表表示，用链表Node中的边只需用头节点存储即可）
class Edge {
    int n, w;
    public Edge(int node, int weight) {
        n = node;
        w = weight;
    }
}

public Node[] createGraph(int[][] matrix, int n) {
    Node[] graph = new Node[n];
    for (int i = 0; i < n; i++) {
        graph[i] = new Node();
    }
    for (int i = 0; i < matrix.length; i++) {
        int weight = matrix[i][0], from = matrix[i][1], to = matrix[i][2];
        graph[from].edges.add(new Edge(to, weight));
    }
    return graph;
}

c++版本

1
2
3
4
5
// 定义边数据结构，存储边到达的下一个顶点和权重
struct Edge { int n, w; };
// 邻接表表示图，可以用两个vector表示，也可以用一个存储vector的数组表示
vector<vector<Edge>> g(n);
// vector<Edge> g[n];

4.2 宽度优先遍历

如下所示的图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static void bfs(Graph graph) {
    Queue<Node> queue = new LinkedList<>();
    // 用于判断顶点是否访问过
    Set<Node> visited = new HashSet<>();
    // 随便选一个顶点作为开始顶点
    visited.add(graph.nodes.get(0));
    queue.add(graph.nodes.get(0));
    while (!queue.isEmpty()) {
        Node node = queue.remove();
        System.out.println(node.value);
        for (Node nextNode : node.nextNodes) {
            if (!visited.contains(nextNode)) {
                visited.add(nextNode);
                queue.add(nextNode);
            }
        }
    }
}

4.3 深度优先遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static void dfs(Graph graph) {
    Node node = graph.nodes.get(0);
    Set<Node> visited = new HashSet<>();
    visited.add(node);
    recur(node, visited);
}

public static void recur(Node node, Set<Node> visited) {
    System.out.println(node.value);
    for (Node nextNode : node.nextNodes) {
        if (!visited.contains(nextNode)) {
            visited.add(nextNode);
            recur(nextNode, visited);
        }
    }
}

4.4 拓扑排序

课表排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        Node[] g = new Node[numCourses];
        for (int i = 0; i < numCourses; i++) {
            g[i] = new Node();
        }
        int[] in = new int[numCourses];
        for (int[] prereq : prerequisites) {
            g[prereq[1]].edges.add(prereq[0]);
            in[prereq[0]]++;
        }
        int cnt = 0;
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < in.length; i++) {
            if (in[i] == 0) {
                queue.add(i);
                cnt++;
            }
        }
        while (!queue.isEmpty()) {
            int node = queue.remove();
            for (int n : g[node].edges) {
                in[n]--;
                if (in[n] == 0) {
                    queue.add(n);
                    cnt++;
                }
            }
        }
        return cnt == numCourses;
    }
}
// 边只表示下一个顶点即可，因此不需要单独创建边类
class Node {
    List<Integer> edges = new ArrayList<>();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// directed graph and no loop
public static List<Node> sortedTopology(Graph graph) {
    // key 某个节点   value 剩余的入度
    HashMap<Node, Integer> inMap = new HashMap<>();
    // 只有剩余入度为0的点，才进入这个队列
    Queue<Node> zeroInQueue = new LinkedList<>();
    for (Node node : graph.nodes.values()) {
        inMap.put(node, node.in);
        if (node.in == 0) {
            zeroInQueue.add(node);
        }
    }
    List<Node> result = new ArrayList<>();
    while (!zeroInQueue.isEmpty()) {
        Node cur = zeroInQueue.poll();
        result.add(cur);
        for (Node next : cur.nexts) {
            inMap.put(next, inMap.get(next) - 1);
            if (inMap.get(next) == 0) {
                zeroInQueue.add(next);
            }
        }
    }
    return result;
}

4.5 Kruskal算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 存储每个顶点的父顶点
public static HashMap<Integer, Integer> parent = new HashMap<>();
// 查询顶点x的父顶点，同时在查询过程中修改结构使得提高查询速度
public static int find(int x) {
    if (parent.get(x) != x) {
        parent.put(x, find(parent.get(x)));
    }
    return parent.get(x);
}

public static void kruskal(Graph graph) {
    for (Node node : graph.nodes.values()) {
        parent.put(node.value, node.value);
    }
    // 优先队列保证每次取出的是最小值
    Queue<Edge> queue = new PriorityQueue<>((o1, o2) -> o1.weight - o2.weight);
    queue.addAll(graph.edges);
    while (!queue.isEmpty()) {
        Edge edge = queue.remove();
        int from = find(edge.from.value);
        int to = find(edge.to.value);
        // 如果两个顶点的父顶点不同，说明连接起来不会形成环
        if (from != to) {
            parent.put(from, to);
            System.out.println(edge.from.value + " " + edge.to.value + " " + edge.weight);
        }
    }
}

4.6 Prim算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static void prim(Graph graph) {
    Queue<Edge> queue = new PriorityQueue<>();
    Set<Node> visited = new HashSet<>();
    // for循环用于处理图不连通的情况
    for (Node node : graph.nodes.values()) {
        if (visited.contains(node)) {
            continue;
        }
        // 找一个node顶点开始
        visited.add(node);
        // 加入node的所有边
        queue.addAll(node.edges);
        while (!queue.isEmpty()) {
            // 选出解锁的边的最小的边判断
            Edge edge = queue.remove();
            Node to = edge.to;
            // 如果这个边的另一个顶点没有加入，则加入到结果中，同时把新加入的顶点的所有边（新解锁的边）加入到堆中
            if (visited.contains(to)) {
                continue;
            }
            // 如果该顶点是新顶点，则这个边也可以加入到最小生成树的边中
            visited.add(to);
            System.out.println(edge.from.value + " " + edge.to.value + " " + edge.weight);
            queue.addAll(to.edges);
        }
    }
}

4.7 前缀Trie树

trie前缀树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class Trie {
    boolean isEnd = false;
    Trie[] next = new Trie[26];

    public Trie() {
        
    }
    
    public void insert(String word) {
        if (search(word)) {
            return;
        }
        char[] words = word.toCharArray();
        Trie cur = this;
        for (char ch : words) {
            int index = ch - 'a';
            if (cur.next[index] == null) {
                cur.next[index] = new Trie();
            }
            cur = cur.next[index];
        }
        cur.isEnd = true;
    }
    
    public boolean search(String word) {
        Trie cur = this;
        char[] words = word.toCharArray();
        for (char ch : words) {
            int index = ch - 'a';
            if (cur.next[index] == null) {
                return false;
            }
            cur = cur.next[index];
        }
        return cur.isEnd;
    }
    
    public boolean startsWith(String prefix) {
        Trie cur = this;
        char[] words = prefix.toCharArray();
        for (char ch : words) {
            int index = ch - 'a';
            if (cur.next[index] == null) {
                return false;
            }
            cur = cur.next[index];
        }
        return true;
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
class Trie {
public:
    vector<Trie*> next;
    bool is_end;
    Trie() : next(26), is_end(false) {}
    // c++需要手动释放内存，因为next数组中的指针是new出来的，否则会造成内存泄漏
    // 虽然算法题是一次运行，基本不会出现内存泄漏，但是在笔试面试中尽可能完善，所以需要手动释放
    ~Trie() {
        for (auto &p : next) {
            if (p != nullptr) {
                delete p;
            }
        }
    }
    
    void insert(string word) {
        if (search(word)) {
            return;
        }
        Trie *cur = this;
        for (auto &ch : word) {
            int index = ch - 'a';
            if (cur->next[index] == nullptr) {
                // 这里进行了new操作申请了空间，需要在析构函数中释放掉
                cur->next[index] = new Trie();
            }
            cur = cur->next[index];
        }
        cur->is_end = true;
    }
    
    bool search(string word) {
        Trie *cur = this;
        for (auto &ch : word) {
            int index = ch - 'a';
            if (cur->next[index] == nullptr) {
                return false;
            }
            cur = cur->next[index];
        }
        return cur->is_end;
    }
    
    bool startsWith(string prefix) {
        Trie *cur = this;
        for (auto &ch : prefix) {
            int index = ch - 'a';
            if (cur->next[index] == nullptr) {
                return false;
            }
            cur = cur->next[index];
        }
        return true;
    }
};

/**
 * Your Trie object will be instantiated and called as such:
 * Trie* obj = new Trie();
 * obj->insert(word);
 * bool param_2 = obj->search(word);
 * bool param_3 = obj->startsWith(prefix);
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
public class Code01_Trie {

	// 测试链接 : https://leetcode.cn/problems/implement-trie-ii-prefix-tree/
	// 提交Trie类可以直接通过
	// 原来代码是对的，但是既然找到了直接测试的链接，那就直接测吧
	// 这个链接上要求实现的功能和课上讲的完全一样
	// 该前缀树的路用数组实现
	class Trie {

		class Node {
			public int pass;
			public int end;
			public Node[] nexts;

			public Node() {
				pass = 0;
				end = 0;
				nexts = new Node[26];
			}
		}

		private Node root;

		public Trie() {
			root = new Node();
		}

		public void insert(String word) {
			if (word == null) {
				return;
			}
			char[] str = word.toCharArray();
			Node node = root;
			node.pass++;
			int path = 0;
			for (int i = 0; i < str.length; i++) { // 从左往右遍历字符
				path = str[i] - 'a'; // 由字符，对应成走向哪条路
				if (node.nexts[path] == null) {
					node.nexts[path] = new Node();
				}
				node = node.nexts[path];
				node.pass++;
			}
			node.end++;
		}

		public void erase(String word) {
			if (countWordsEqualTo(word) != 0) {
				char[] chs = word.toCharArray();
				Node node = root;
				node.pass--;
				int path = 0;
				for (int i = 0; i < chs.length; i++) {
					path = chs[i] - 'a';
					if (--node.nexts[path].pass == 0) {
						node.nexts[path] = null;
						return;
					}
					node = node.nexts[path];
				}
				node.end--;
			}
		}

		public int countWordsEqualTo(String word) {
			if (word == null) {
				return 0;
			}
			char[] chs = word.toCharArray();
			Node node = root;
			int index = 0;
			for (int i = 0; i < chs.length; i++) {
				index = chs[i] - 'a';
				if (node.nexts[index] == null) {
					return 0;
				}
				node = node.nexts[index];
			}
			return node.end;
		}

		public int countWordsStartingWith(String pre) {
			if (pre == null) {
				return 0;
			}
			char[] chs = pre.toCharArray();
			Node node = root;
			int index = 0;
			for (int i = 0; i < chs.length; i++) {
				index = chs[i] - 'a';
				if (node.nexts[index] == null) {
					return 0;
				}
				node = node.nexts[index];
			}
			return node.pass;
		}
	}

}

4.8 迪杰斯特拉算法

网络延迟时间

  1. 普通算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public static Map<Node, Integer> dijkstra(Graph graph) {
    // 保存起始顶点到每个顶点的距离，如果没有则认为距离为正无穷
    Map<Node, Integer> distanceMap = new HashMap<>();
    // 设置0为起始顶点
    Node minNode = graph.nodes.get(0);
    // 起始顶点到自己的距离为0
    distanceMap.put(minNode, 0);
    // 保存哪些顶点加入到判断完的集合中（距离已经是最短的）
    Set<Node> visited = new HashSet<>();
    while (minNode != null) {
        Integer distance = distanceMap.get(minNode);
        for (Edge edge : minNode.edges) {
            // 如果不存在则表示起始顶点到edge.to顶点距离为正无穷，直接添加
            // 如果存在则需要判断  起始顶点直接到edge.to顶点的距离  和
            // 起始顶点到minNode顶点加上minNode到edge.to的距离哪个更小
            if (!distanceMap.containsKey(edge.to)) {
                distanceMap.put(edge.to, distance + edge.weight);
            } else {
                distanceMap.put(edge.to, Math.min(distance + edge.weight, distanceMap.get(edge.to)));
            }
        }
        // 更新结束，将minNode加入集合中
        visited.add(minNode);
        // minNode置为null，(重要)，后续循环退出条件是通过判断minNode是否为空
        minNode = null;
        // 保存最小距离
        int minDist = Integer.MAX_VALUE;
        // 遍历所有的距离，在没有判断确定的顶点中选择距离最短的
        for (Map.Entry<Node, Integer> entry : distanceMap.entrySet()) {
            Node node = entry.getKey();
            Integer dist = entry.getValue();
            // 如果已经是判断过的顶点则直接跳过
            if (!visited.contains(node) && minDist > dist) {
                minDist = dist;
                minNode = node;
            }
        }
    }
    return distanceMap;
}

另一种方式（推荐），图存储方式简单些

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        Node[] g = new Node[n];
        for (int i = 0; i < n; i++) {
            g[i] = new Node();
        }
        for (int[] time : times) {
            g[time[0] - 1].edges.add(new Edge(time[1] - 1, time[2]));
        }
        int[] dist = new int[n];
        Arrays.fill(dist, 0x3f3f3f3f);
        boolean[] st = new boolean[n];
        dist[k - 1] = 0;
        for (int i = 0; i < n - 1; i++) {
            int t = -1;
            for (int j = 0; j < n; j++) {
                if (!st[j] && (t == -1 || dist[t] > dist[j])) {
                    t = j;
                }
            }
            st[t] = true;
            for (Edge edge : g[t].edges) {
                dist[edge.n] = Math.min(dist[edge.n], dist[t] + edge.w);
            }
        }
        int maxDist = Arrays.stream(dist).max().getAsInt();
        return maxDist == 0x3f3f3f3f ? -1 : maxDist;
    }
}

class Edge {
    int n, w;
    public Edge(int node, int weight) {
        n = node;
        w = weight;
    }
}

class Node {
    List<Edge> edges = new ArrayList<>();
}

another cpp版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    struct Edge {
        int n, w;
    };
    int INF = 0x3f3f3f3f;
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        // 两个vector表示邻接表
        // vector<vector<Edge>> g(n);
        // 或者vector<Edge>数组表示邻接表
        vector<Edge> g[n];
        // foreach循环使用引用提高速度
        for (auto &time : times) {
            g[time[0] - 1].push_back({time[1] - 1, time[2]});
        }
        int dist[n];
        bool st[n];
        memset(dist, 0x3f, sizeof dist);
        memset(st, 0, sizeof st);
        dist[k - 1] = 0;
        for (int i = 0; i < n - 1; i++) {
            int t = -1;
            for (int j = 0; j < n; j++) {
                if (!st[j] && (t == -1 || dist[t] > dist[j])) {
                    t = j;
                }
            }
            st[t] = true;
            for (auto &edge : g[t]) {
                dist[edge.n] = min(dist[edge.n], dist[t] + edge.w);
            }
        }
        int maxDist = *max_element(dist, dist + n);
        return maxDist == INF ? -1 : maxDist;
    }
};
  1. 优化算法

5 贪心算法

5.1 会议安排

LeetCode 646

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int findLongestChain(int[][] pairs) {
        Arrays.sort(pairs, (a, b) -> a[1] - b[1]);
        int retLength = 0, curTime = Integer.MIN_VALUE;
        for (int[] pair : pairs) {
            if (curTime < pair[0]) {
                retLength++;
                curTime = pair[1];
            }
        }
        return retLength;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Program {
    int start, end;
}

public static int maxMeetings(Program[] programs) {
    // 按照结束时间排序
    Arrays.sort(programs, (p1, p2) -> p1.end - p2.end);
    int timePoint = programs[0].start;
    int ret = 0;
    for (int i = 0; i < programs.length; i++) {
        if (timePoint <= programs[i].start) {
            timePoint = programs[i].end;
            ret++;
        }
    }
    return ret;
}

5.2 字符串数组排序

1
2
3
4
public static void sortString(String[] strs) {
    // 按照两个字符串不同拼接方式排序
    Arrays.sort(strs, (s1, s2) -> (s1 + s2).compareTo(s2 + s1));
}

5.3 金条划分

按照上图中的两个不同分割法：

  • 第一种：先划分为10和50，消耗60，再划分为20和30，消耗50，总计110。
  • 第二种：先划分为30和30，消耗60，再划分为10和20，消耗30，总计90。

如果要取到最小的，需要先按照最大的划分，逆向过来，这是一颗哈夫曼树。

1
2
3
4
5
6
7
8
9
10
11
12
13
public static int lessMoney(int[] arr) {
    Queue<Integer> heap = new PriorityQueue<>();
    for (int a : arr) {
        heap.add(a);
    }
    int cur = 0, sum = 0;
    while (heap.size() > 1) {
        cur = heap.remove() + heap.remove();
        sum += cur;
        heap.add(cur);
    }
    return sum;
}

5.4 利润最大

LeetCode 502

先按照成本花费升序排序，每一轮选出可以做的（成本不大于当前资金的）项目，加入到另一个集合中保存，选出利润最大的做，然后更新当前可用资金。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
        Queue<Pair> capHeap = new PriorityQueue<>((p1, p2) -> p1.c - p2.c);
        Queue<Pair> proHeap = new PriorityQueue<>((p1, p2) -> p2.p - p1.p);
        for (int i = 0; i < profits.length; i++) {
            capHeap.add(new Pair(profits[i], capital[i]));
        }
        for (int i = 0; i < k; i++) {
            while (!capHeap.isEmpty() && capHeap.peek().c <= w) {
                proHeap.add(capHeap.remove());
            }
            if (proHeap.isEmpty()) {
                return w;
            }
            w += proHeap.remove().p;
        }
        return w;
    }
}

class Pair {
    int p, c;
    public Pair(int p, int c) {
        this.p = p;
        this.c = c;
    }
}

5.5 数据流的中位数(堆的应用)

LeetCode 295

用两个堆，一个大根堆一个小根堆，其中大根堆保存小于等于中位数部分的数据，小根堆保存大于中位数部分的数据。

插入数据算法流程：

  1. 如果大根堆空，直接加入大根堆，结束，否则执行2
  2. 如果小于等于大根堆堆顶，加入大根堆，否则加入小根堆
  3. 判断大小根堆数据量差值，如果插值大于1，则将数据量多的堆的堆顶弹出加入到另一个堆中

查询算法流程：

  1. 如果两个堆数据量相同，则大小根堆查询堆顶相加除以2，得到中位数，结束，否则执行2
  2. 返回数据量大的堆的堆顶元素
5.5-1.drawio.svg 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class MedianFinder {

    private Queue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
    private Queue<Integer> minHeap = new PriorityQueue<>();

    public MedianFinder() {

    }
    
    public void addNum(int num) {
        if (maxHeap.isEmpty()) {
            maxHeap.add(num);
            return;
        }
        if (num <= maxHeap.peek()) {
            maxHeap.add(num);
        } else {
            minHeap.add(num);
        }
        if (maxHeap.size() - minHeap.size() > 1) {
            minHeap.add(maxHeap.remove());
        } else if (minHeap.size() - maxHeap.size() > 1) {
            maxHeap.add(minHeap.remove());
        }
    }
    
    public double findMedian() {
        if (maxHeap.size() == minHeap.size()) {
            return (maxHeap.peek() + minHeap.peek()) / 2.0;
        }
        if (maxHeap.size() > minHeap.size()) {
            return maxHeap.peek();
        } else {
            return minHeap.peek();
        }
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */

6 暴力递归

LeetCode 940

6.1 字符串全排列

LeetCode 46

  1. 不去重
  2. 去重
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public static List<String> permutation3(String s) {
    List<String> ans = new ArrayList<>();
    if (s == null || s.length() == 0) {
        return ans;
    }
    char[] str = s.toCharArray();
    g2(str, 0, ans);
    return ans;
}

public static void g2(char[] str, int index, List<String> ans) {
    if (index == str.length) {
        ans.add(String.valueOf(str));
    } else {
        boolean[] visited = new boolean[256];
        for (int i = index; i < str.length; i++) {
            // 不去重删除掉这个if判断代码即可
            if (!visited[str[i]]) {
                visited[str[i]] = true;
                swap(str, index, i);
                g2(str, index + 1, ans);
                swap(str, index, i);
            }
        }
    }
}

6.2 预测赢家

LeetCode 486

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public boolean predictTheWinner(int[] nums) {
        return dfs(nums, 0, nums.length - 1) >= 0;
    }

    private int dfs(int[] nums, int i, int j) {
        if (i == j) {
            return nums[i];
        }
        int left = nums[i] - dfs(nums, i + 1, j);
        int right = nums[j] - dfs(nums, i, j - 1);
        return Math.max(left, right);
    }
}

可以设置两个函数，分别为先手和后手函数。记为f(arr, l, r)和s(arr, l, r)分别表示在arr中的l和r范围内进行决策得到的结果。

1
2
3
4
5
6
7
8
9
int f(arr, l, r) {
    // 如果只有一个数，那么先手只能拿这一个
    if (l == r) {
        return arr[l];
    }
    // 否则有两种决策情况，一种是拿最左侧，一种是拿最右侧
    // 而拿完后，剩下的数对于当前来说属于后手，所以调用后手函数，而为了保证当前分数为最大值，所以使用max取最大值
    return max(arr[l] + s(arr, l + 1, r), arr[r] + s(arr, l, r - 1));
}
1
2
3
4
5
6
7
8
9
10
int s(arr, l, r) {
    // 如果为后手，只有一个数，那么先手会拿到这个数，后手没得拿只能返回0
    if (l == r) {
        return 0;
    }
    // 后手拿[l, r]范围内的数，只有两种可能，因为先手只能拿最左侧或最右侧。
    // 先手拿完后，后手变成了先手，所以调用先手函数。
    // 而同时两个人都保证分数最大化，所以先手拿完后肯定要保证后手是分数最小化，所以需要取最小值。
    return min(f(arr, l + 1, r), f(arr, l, r - 1));
}

1423. 可获得的最大点数 - 力扣（LeetCode）

6.3 解码方法

LeetCode 91

递归方法（会超时）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int numDecodings(String s) {
        return numDecodings(s.toCharArray(), 0);
    }

    public int numDecodings(char[] chs, int i) {
        if (i == chs.length) {
            return 1;
        }
        if (chs[i] == '0') {
            return 0;
        }
        int ret = numDecodings(chs, i + 1);
        if (chs[i] == '1') {
            if (i + 1 < chs.length) {
                ret += numDecodings(chs, i + 2);
            }
        }
        if (chs[i] == '2') {
            if (i + 1 < chs.length && chs[i + 1] < '7') {
                ret += numDecodings(chs, i + 2);
            }
        }
        return ret;
    }
}

6.4 n皇后问题

常规方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 当前来到i行，一共是0~N-1行
// 在i行上放皇后，所有列都尝试
// 必须要保证跟之前所有的皇后不打架
// int[] record record[x] = y 之前的第x行的皇后，放在了y列上
// 返回：不关心i以上发生了什么，i.... 后续有多少合法的方法数
public static int process1(int i, int[] record, int n) {
    if (i == n) {
        return 1;
    }
    int res = 0;
    // i行的皇后，放哪一列呢？j列，
    for (int j = 0; j < n; j++) {
        if (isValid(record, i, j)) {
            record[i] = j;
            res += process1(i + 1, record, n);
        }
    }
    return res;
}

public static boolean isValid(int[] record, int i, int j) {
    // 0..i-1
    for (int k = 0; k < i; k++) {
        // 判断是不是在同一列或者是在同一斜线上，此处用斜率判断，1或者-1
        if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
            return false;
        }
    }
    return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 请不要超过32皇后问题
public static int num2(int n) {
    if (n < 1 || n > 32) {
        return 0;
    }
    // 如果你是13皇后问题，limit 最右13个1，其他都是0
    int limit = n == 32 ? -1 : (1 << n) - 1;
    return process2(limit, 0, 0, 0);
}

// 7皇后问题
// limit : 0....0 1 1 1 1 1 1 1
// 之前皇后的列影响：colLim
// 之前皇后的左下对角线影响：leftDiaLim
// 之前皇后的右下对角线影响：rightDiaLim
public static int process2(int limit, int colLim, int leftDiaLim, int rightDiaLim) {
    if (colLim == limit) {
        return 1;
    }
    // pos中所有是1的位置，是你可以去尝试皇后的位置
    int pos = limit & (~(colLim | leftDiaLim | rightDiaLim));
    int mostRightOne = 0;
    int res = 0;
    while (pos != 0) {
        mostRightOne = pos & (~pos + 1);
        pos = pos - mostRightOne;
        res += process2(limit, colLim | mostRightOne, (leftDiaLim | mostRightOne) << 1,
                        (rightDiaLim | mostRightOne) >>> 1);
    }
    return res;
}

打印所有可能的n皇后解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import java.util.*;

class Main {
    public static StringBuilder sb = new StringBuilder();
    public static char[][] g;
    public static int[] record;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        g = new char[n][n];
        record = new int[n];
        Arrays.fill(record, -1);
        for (int i = 0; i < n; i++) {
            Arrays.fill(g[i], '.');
        }
        recur(0, n);
        sc.close();
    }
    
    public static void recur(int i, int n) {
        if (i == n) {
            // 清空sb内容。
            sb.setLength(0);
            for (int k = 0; k < n; k++) {
                for (int j = 0; j < n; j++) {
                    sb.append(g[k][j]);
                }
                sb.append('\n');
            }
            System.out.println(sb);
        } else {
            for (int j = 0; j < n; j++) {
                if (isValid(i, j)) {
                    record[i] = j;
                    g[i][j] = 'Q';
                    recur(i + 1, n);
                    g[i][j] = '.';
                    record[i] = -1;
                }
            }
        }
    }
    
    public static boolean isValid(int i, int j) {
        // (i, j) (k, record[k])
        for (int k = 0; k < i; k++) {
            if (j == record[k] || Math.abs(i - k) == Math.abs(j - record[k])) {
                return false;
            }
        }
        return true;
    }
}

51. N 皇后 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {

    public List<List<String>> solveNQueens(int n) {
        List<List<String>> ret = new ArrayList<>();
        char[][] g = new char[n][n];
        StringBuilder sb = new StringBuilder();
        int[] record = new int[n];
        Arrays.fill(record, -1);
        for (int i = 0; i < n; i++) {
            Arrays.fill(g[i], '.');
        }
        dfs(0, n, g, record, ret);
        return ret;
    }
    public void dfs(int i, int n, char[][] g, int[] record, List<List<String>> ret) {
        if (i == n) {
            List<String> temp = new ArrayList<>();
            for (int j = 0; j < n; j++) {
                temp.add(String.valueOf(g[j]));
            }
            ret.add(temp);
            return;
        }
        for (int j = 0; j < n; j++) {
            if (isValid(i, j, record)) {
                record[i] = j;
                g[i][j] = 'Q';
                dfs(i + 1, n, g, record, ret);
                g[i][j] = '.';
                record[i] = -1;
            }
        }
    }
    public boolean isValid(int i, int j, int[] record) {
        for (int k = 0; k < i; k++) {
            if (j == record[k] || Math.abs(i - k) == Math.abs(j - record[k])) {
                return false;
            }
        }
        return true;
    }
}

7 哈希函数与哈希表

哈希函数的性质（简要记录）：

  1. 无穷多的值映射到有范围的值
  2. 相同的输入得到相同的输出
  3. 不同的输入可能得到相同的输出
  4. 映射后的值分布比较均匀

7.1 例题

题目：如果有一个40亿条记录的大文件，现需要求出现次数最多的记录，限制内存使用为1GB。
解法：如果直接采用哈希表的方式按照（记录，次数）的方式存储每个记录的次数，内存肯定会不够。因此采用哈希函数首先将记录做一次哈希，然后将得到的值模100，最后肯定会得到一个0-99的值，按照模除后的结果将该条记录存到对应的小文件中，再对每个小文件使用哈希表的方式进行统计（此时的内存空间是够用的）。

❗如果采用摩尔投票法需要保证重复的记录超过总记录数的一半。

7.2 布隆过滤器

主要用于类似黑名单系统，查找当前记录是否存在于“黑名单”中，并且这个黑名单只会添加记录，不会删除记录，使用布隆过滤器可以比使用hash表大大减少空间。但是布隆过滤器存在一定的失误率，即不存在于黑名单的记录可能也会认为是黑名单，可以通过设置大小大大降低失误率，但是失误率是一直存在的。
使用到的数据结构：二进制位组成的集合。
算法过程：

  1. 准备个哈希函数
  2. 添加黑名单
    1. 遍历黑名单记录列表
      1. 遍历哈希函数
        1. 每个哈希函数求得一个哈希值
        2. 将位集合中的位设置为1
  3. 判断是否在黑名单中
    1. 对于一个记录遍历哈希函数
      1. 求得一个哈希值
      2. 判断是否为1
    2. 当所有的位置都为1时说明在黑名单中（可能存在失误），否则不在

首先需要构造一个二进制位集合，这里可以采用int数组的形式，每一个值表示32位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 设总共需要m位的集合
// 上取整
int a[ceil(m / 32)];
// 将第i位设置为1
void setI1(int *a, int i) {
    int index = i / 32, bit_index = i % 32;
    a[index] = a[index] | (1 << bit_index);
}
// 将第i位设置为0
void setI0(int *a, int i) {
    int index = i / 32, bit_index = i % 32;
    a[index] = a[index] & (~(1 << bit_index))
}
// 获取第i位的值（0或1）
int getI(int *a, int i) {
    int index = i / 32, bit_index = i % 32;
    return (a[index] >> bit_index) & 1;
}

🍰位的集合长度和个哈希函数怎么确定和的值呢？
可以用三个公式来确定，首先给定样本量（即黑名单数量）和失误率，有：


真真真真
前两个公式计算出的是理论上的集合长度和理论上的哈希函数个数，实际中集合长度可以更大一些即真，而哈希函数个数需要采用上取整的方式即真，以此再次求得真实的失误率。

7.3 一致性哈希

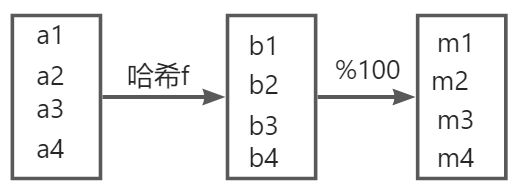
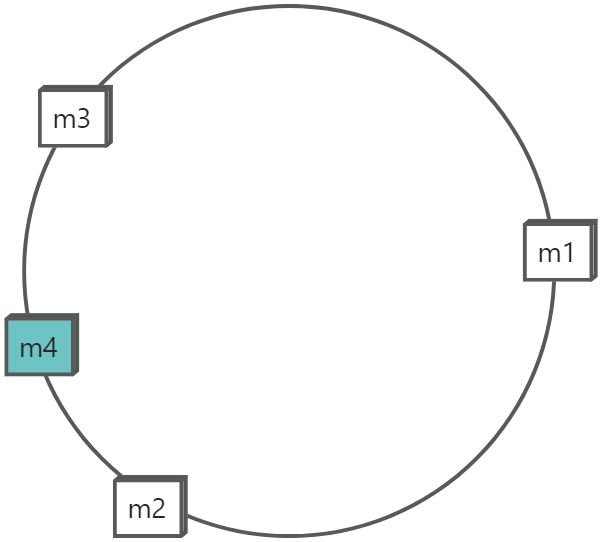
服务器利用hash key进行划分做负载均衡，尽量选取种类多，且分布较均匀的key。否则会导致某些服务器资源利用过多（如某些key使用很多，但另一些使用很少）。如果后期需要增加服务器或者减少，则会导致数据迁移，而这个数据迁移是全量的迁移。
为了解决数据迁移的问题，可以将进行hash运算过后的数值范围看作一个环，将服务器分配到hash环上，然后访问或添加时，计算hash值后，判断结果距离哪个服务器的hash值最近（可以统一采用顺时针的方式），这样之后如果要添加服务器m4（假设计算后位于m2和m3中间），数据只需要迁移m2和m4之间的数据到m4中即可。大大减小了迁移量，但是这会引起新的问题：

  1. 无法保证初始分配的节点比较少时是均匀分配的（hash计算能保证大数据量的情况下是均分的）
  2. 添加一个节点后也不能保证添加之后是均分的


解决方式：虚拟节点
假设m1有1000个（虚拟）节点名称：(a1, a2, a3, ..., a1000），m2和m3同理
将这3000个虚拟节点计算hash后分布到hash环中，数据量较大，可以保证分配比较均匀。
同时如果加入节点，也是按照虚拟节点加入，也能保证加入后的分布较均匀。
还有一个好处是，如果m1的性能较好，可以给m1设置较多的虚拟节点，让更多的数据分配到m1，如果m3性能较差可以分配较少的虚拟节点，以进行服务器负载的管理。

8 有序表、并查集

image.png
岛屿问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int getIsland(vector<vector<int>> &m, int N, int M) {
    int ret = 0;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            if (m[i][j] == 1) {
                ret++;
                dfs(m, i, j, N, M);
            }
        }
    }
    return ret;
}

void dfs(vector<vector<int>> &m, int i, int j, int N, int M) {
    if (i < 0 || i >= N || j < 0 || j >= M || m[i][j] == 0) {
        return;
    }
    m[i][j] = 2;
    dfs(m, i - 1, j, N, M);
    dfs(m, i, j - 1, N, M);
    dfs(m, i + 1, j, N, M);
    dfs(m, i, j + 1, N, M);
}

时间复杂度
⭐进阶：利用并行算法解决这个问题
视频链接：左神视频链接

8.1 并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class UnionFind {
    private int[] p;
    public UnionFind(int n) {
        // 初始化，设置每个元素的父元素都为自己
        p = new int[n];
        for (int i = 0; i < n; i++) {
            p[i] = i;
        }
    }
    // 查找
    public int find(int x) {
        if (x != p[x]) {
            // 查找同时优化节点，减少树的层数
            p[x] = find(p[x]);
        }
        return p[x];
    }
    // 合并
    public void union(int a, int b) {
        int pa = find(a);
        int pb = find(b);
        if (pa != pb) {
            p[pa] = pb;
        }
    }
}

9 KMP算法

左神算法笔记
2024/09/23/左神算法笔记/左神算法笔记/
作者
yatbfm
发布于
2024-09-23 21:39
许可
  1. 1 时间复杂度和排序算法
    1. 1.1 交换两个数的写法
    2. 1.2 找到数组中出现奇数次的数字
      1. 1.2.1 假设只有一种数出现奇数次
      2. 1.2.2 假设有两种数出现奇数次
    3. 1.3 插入排序
    4. 1.4 Master公式
    5. 1.5 归并排序
    6. 1.6 快速排序
    7. 1.7 堆
    8. 1.8 堆排序扩展题
    9. 1.9 基数排序
  2. 2 链表
    1. 2.1 回文链表的判断
      1. 方法一
      2. 方法二
    2. 2.2 随机链表的复制
      1. 方法一
      2. 方法二
    3. 2.3 判断一个链表是否有环，以及返回入环节点
      1. 方法一
      2. 方法二
    4. 2.4 判断两个链表是否相交
    5. 2.5 找到两个有序链表相同的节点
    6. 2.6 把链表按某个值分为小于 等于 大于的部分
      1. 入门做法
      2. 高级做法
      3. 链表快速排序
      4. 链表归并排序
  3. 3 二叉树
    1. 3.1 遍历
      1. 3.1.1 前中后序遍历（非递归）
      2. 3.1.2 层序遍历
    2. 3.2 求二叉树一层最多的节点个数（每一层的节点个数）
    3. 3.3 二叉树的最大宽度
    4. 3.4 判断是否是完全二叉树
    5. 3.5 判断满二叉树
    6. 3.6 判断平衡二叉树
    7. 3.7 判断是否是二叉搜索树
    8. 3.8 找到二叉树两个节点的最低公共祖先节点
    9. 3.9 二叉搜索树的中序后继
    10. 3.10 二叉树的序列化与反序列化
    11. 3.11 判断是否是二叉树
  4. 4 图
    1. 4.1 图的存储
    2. 4.2 宽度优先遍历
    3. 4.3 深度优先遍历
    4. 4.4 拓扑排序
    5. 4.5 Kruskal算法
    6. 4.6 Prim算法
    7. 4.7 前缀Trie树
    8. 4.8 迪杰斯特拉算法
  5. 5 贪心算法
    1. 5.1 会议安排
    2. 5.2 字符串数组排序
    3. 5.3 金条划分
    4. 5.4 利润最大
    5. 5.5 数据流的中位数(堆的应用)
  6. 6 暴力递归
    1. 6.1 字符串全排列
    2. 6.2 预测赢家
    3. 6.3 解码方法
    4. 6.4 n皇后问题
  7. 7 哈希函数与哈希表
    1. 7.1 例题
    2. 7.2 布隆过滤器
    3. 7.3 一致性哈希
  8. 8 有序表、并查集
    1. 8.1 并查集
  9. 9 KMP算法
© 2020 - 2025    yatbfm
由 Hexo 驱动 & 主题 Keep
访客数 访问量
  1. 1 时间复杂度和排序算法
    1. 1.1 交换两个数的写法
    2. 1.2 找到数组中出现奇数次的数字
      1. 1.2.1 假设只有一种数出现奇数次
      2. 1.2.2 假设有两种数出现奇数次
    3. 1.3 插入排序
    4. 1.4 Master公式
    5. 1.5 归并排序
    6. 1.6 快速排序
    7. 1.7 堆
    8. 1.8 堆排序扩展题
    9. 1.9 基数排序
  2. 2 链表
    1. 2.1 回文链表的判断
      1. 方法一
      2. 方法二
    2. 2.2 随机链表的复制
      1. 方法一
      2. 方法二
    3. 2.3 判断一个链表是否有环，以及返回入环节点
      1. 方法一
      2. 方法二
    4. 2.4 判断两个链表是否相交
    5. 2.5 找到两个有序链表相同的节点
    6. 2.6 把链表按某个值分为小于 等于 大于的部分
      1. 入门做法
      2. 高级做法
      3. 链表快速排序
      4. 链表归并排序
  3. 3 二叉树
    1. 3.1 遍历
      1. 3.1.1 前中后序遍历（非递归）
      2. 3.1.2 层序遍历
    2. 3.2 求二叉树一层最多的节点个数（每一层的节点个数）
    3. 3.3 二叉树的最大宽度
    4. 3.4 判断是否是完全二叉树
    5. 3.5 判断满二叉树
    6. 3.6 判断平衡二叉树
    7. 3.7 判断是否是二叉搜索树
    8. 3.8 找到二叉树两个节点的最低公共祖先节点
    9. 3.9 二叉搜索树的中序后继
    10. 3.10 二叉树的序列化与反序列化
    11. 3.11 判断是否是二叉树
  4. 4 图
    1. 4.1 图的存储
    2. 4.2 宽度优先遍历
    3. 4.3 深度优先遍历
    4. 4.4 拓扑排序
    5. 4.5 Kruskal算法
    6. 4.6 Prim算法
    7. 4.7 前缀Trie树
    8. 4.8 迪杰斯特拉算法
  5. 5 贪心算法
    1. 5.1 会议安排
    2. 5.2 字符串数组排序
    3. 5.3 金条划分
    4. 5.4 利润最大
    5. 5.5 数据流的中位数(堆的应用)
  6. 6 暴力递归
    1. 6.1 字符串全排列
    2. 6.2 预测赢家
    3. 6.3 解码方法
    4. 6.4 n皇后问题
  7. 7 哈希函数与哈希表
    1. 7.1 例题
    2. 7.2 布隆过滤器
    3. 7.3 一致性哈希
  8. 8 有序表、并查集
    1. 8.1 并查集
  9. 9 KMP算法