yatbfm's blog
LeetCode Hot100
yatbfm
  2023-12-01 21:39   2025-01-22 11:27    19.2k 字  88 分钟  

盛最多水的容器

https://leetcode.cn/problems/container-with-most-water/?envType=study-plan-v2&envId=top-100-liked
如果使用两层for循环会导致超时。
使用双指针从左右边界向内收缩，依次缩减范围，直到两个指针相遇，具体收缩步骤：

  1. 计算体积，比较大小
  2. 比较左右指针所在位置的高度
  3. 高度低的向内收缩

🍰 证明：
假设左右指针分别为i, j所在位置的高度为x, y，用S(i, j)表示指针位置形成的体积大小。这里假设x < y。如果按照上述收缩思路的话，应该是i向右移，形成的体积大小是S(i + 1, j)。这里会有疑问的是丢失了S(i, j - 1), S(i, j - 2), ..., S(i, i + 1)的状态。下面证明这些状态都小于S(i, j)。
首先设j - i的长度为w，然后丢失状态的所有容器的长度(j - t) - i设为w'都一定小于w。
丢失状态中的i指针不动，高度为x，右指针向内收缩，高度设为y'，可以知道y'和y的大小关系不确定。分为两种情况：

  1. y' > y，那么S(i, j - t)的体积为w' * x，一定小于S(i, j) = w * x。
  2. y' <= y，那么S(i, j - t)的体积为min(x, y') * w'
    1. x > y'，S(i, j - t) = y' * w'一定小于w * x
    2. x <= y'，S(i, j - t) = x * w'一定小于w * x

所以如果移动高位置的指针，一定会导致容器体积减小，移动低位置的可能会使得容器体积增大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int maxArea(int[] height) {
        int result = 0;
        for (int i = 0, j = height.length - 1; i < j;) {
            result = Math.max(result, Math.min(height[i], height[j]) * (j - i));
            if (height[i] < height[j]) {
                i++;
            } else {
                j--;
            }
        }
        return result;
    }
}

三数之和

https://leetcode.cn/problems/3sum/description/?envType=study-plan-v2&envId=top-100-liked
如果使用三层for循环会超时。
这里使用双指针，首先对数组进行排序，然后固定指针k，取另外两个指针i j分别在k + 1, nums.length - 1的位置，然后判断：

  1. nums[k] + nums[i] + nums[j] > 0则整体偏大，需要减小，可以让j--
  2. nums[k] + nums[i] + nums[j] < 0则整体偏小，需要增大，可以让i++
  3. 否则满足条件，加入结果列表

这里需要注意要排除重复的三元组，因此在移动指针时需要判断后续判断的值是否和当前值冲突

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> resultList = new ArrayList<>();
        for (int k = 0; k < nums.length; k++) {
            // 排除重复元素，如果k和k-1位置的数一样，那么后续计算的结果一定一样，因此需要排除
            if (k > 0 && nums[k] == nums[k - 1]) {
                continue;
            }
            // 如果nums[k] > 0，那么nums[i]和nums[j]一定 > 0，结果一定 > 0
            if (nums[k] > 0) {
                return resultList;
            }
            for (int i = k + 1, j = nums.length - 1; i < j;) {
                int temp = nums[i] + nums[j] + nums[k];
                if (temp > 0) {
                    // 跳过重复数值，只取重复的最后一个
                    while (i < j && nums[j] == nums[--j]);
                } else if (temp < 0) {
                    while (i < j && nums[i] == nums[++i]);
                } else {
                    resultList.add(Arrays.asList(nums[k], nums[i], nums[j]));
                    while (i < j && nums[i] == nums[++i]);
                    while (i < j && nums[j] == nums[--j]);
                }
            }
        }
        return resultList;
    }
}

最长连续序列

https://leetcode.cn/problems/longest-consecutive-sequence/description/?envType=study-plan-v2&envId=top-100-liked
本题要求时间复杂度为O(n)，如果直接排序的话复杂度达到O(nlogn)。
要找出连续序列的长度，可以换个思路，如果找到一个数nums[i]，然后将这个数一直+1，加完后的数在数组里还能找到那就说明连续序列的长度可以增加 1。因此满足这个条件的话需要使用到哈希，将所有的数保存在一个集合中，方便查询。
这里的一个优化是如果当前数减 1 之后还能在数组中找到，那么可以直接跳过，因为减 1 之后的数在计算序列长度时已经包含了当前数，从当前数开始计算的长度一定不如减 1 之后的数计算的序列长度长。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int longestConsecutive(int[] nums) {
        Set<Integer> numSet = new HashSet<>();
        for (int num : nums) {
            numSet.add(num);
        }
        int result = 0;
        for (int num : nums) {
            // 如果包含减1之后的数，那么直接跳过，因为之前已经计算过
            if (numSet.contains(num - 1)) {
                continue;
            }
            int tempResult = 1;
            int temp = num;
            // 如果加1后还在数组里能找到，序列长度加1
            while (numSet.contains(++temp)) {
                tempResult++;
            }
            // 保存最大的序列长度
            result = Math.max(result, tempResult);
        }
        return result;
    }
}

接雨水

https://leetcode.cn/problems/trapping-rain-water/description/?envType=study-plan-v2&envId=top-100-liked
根据题意，最两侧的柱子不能接到雨水，只能作为墙壁。考虑按列求，单独考虑每个柱子可以接到的雨水。
当前柱子可以接到的雨水由当前柱子左侧和右侧的最高的柱子包裹起来，可以保证接到雨水，而接到的雨水的多少则是右两则最高的柱子中的矮的决定（木桶效应）。如果矮的柱子比当前柱子高，那么接到的雨水就是高度的差值，否则接不到雨水。
那么现在的问题是怎么快速求出当前柱子左侧最高的高度和当前柱子右侧最高的高度。

  1. 动态规划

使用一个数组记录当前位置左侧（不包括自身）最高的高度是多少，即maxLeft[i] = max(maxLeft[i - 1], height[i - 1])，右侧同理
这会使用到O(n)的空间复杂度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int trap(int[] height) {
        int[] maxLeft = new int[height.length];
        int[] maxRight = new int[height.length];
        for (int i = 1; i < height.length; i++) {
            maxLeft[i] = Math.max(maxLeft[i - 1], height[i - 1]);
        }
        for (int i = height.length - 2; i >= 0; i--) {
            maxRight[i] = Math.max(maxRight[i + 1], height[i + 1]);
        }
        int sum = 0;
        for (int i = 1; i < height.length - 1; i++) {
            int min = Math.min(maxLeft[i], maxRight[i]);
            int sub = min - height[i];
            sum += sub > 0 ? sub : 0;
        }
        return sum;
    }
}

无重复字符的最长子串

https://leetcode.cn/problems/longest-substring-without-repeating-characters/?envType=study-plan-v2&envId=top-100-liked
本题可以使用滑动窗口“框住”没有重复字符的子串，遍历完成后最长的窗口长度即为答案。
怎么保证滑动窗口中没有重复字符串呢？使用哈希表存储。
首先使用两个指针j, i为滑动窗口的边界，表示[j, i]区间的字符串都不重复。并且使用一个Set集合保存该窗口中的字符，遍历时如果待加入的字符已经存在了，则一直遍历删除窗口左端的字符直到没有重复的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int lengthOfLongestSubstring(String s) {
        char[] chs = s.toCharArray();
        Set<Character> set = new HashSet<>();
        int result = 0;
        for (int i = 0, j = 0; i < chs.length; i++) {
            while (set.contains(chs[i])) {
                set.remove(chs[j++]);
            }
            set.add(chs[i]);
            result = Math.max(result, set.size());
        }
        return result;
    }
}

和为 K 的子数组

https://leetcode.cn/problems/subarray-sum-equals-k/description/?envType=study-plan-v2&envId=top-100-liked
要求数组中的子数组的和，子数组定义为：连续非空序列。可以理解为一段区间内数值的和，这样可以想到使用前缀和来计算，前缀和数组preSum[i]表示原数组nums中第一个数一直加到第i个数的和，如果表示某一段区间[j, i]的和，计算preSum[i] - preSum[j - 1]即可。
需要注意的是：前缀和数组的长度一般比原数组多一个，多余的一个数表示的是数组中第 0 个数到第 0 个数（即没有任何数的情况下）的和，同时这样做也为了编码简便。
❓ 代码中初始时加入的(0, 1)键值对表示前缀和为 0 的有一个（前缀和中什么数都没有），暂时还不理解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int subarraySum(int[] nums, int k) {
        int n = nums.length;
        int[] preSum = new int[n + 1];
        Arrays.fill(preSum, 0);
        // 计算前缀和，一般下标从1开始，0下标用于表示没有数的时候的前缀和。
        for (int i = 1; i < n + 1; i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
        int result = 0;
        Map<Integer, Integer> mp = new HashMap<>();
        for (int i = 0; i < n + 1; i++) {
            if (mp.containsKey(preSum[i] - k)) {
                result += mp.get(preSum[i] - k);
            }
            mp.put(preSum[i], mp.getOrDefault(preSum[i], 0) + 1);
        }
        return result;
    }
}

滑动窗口最大值

https://leetcode.cn/problems/sliding-window-maximum/?envType=study-plan-v2&envId=top-100-liked
滑动窗口求最大值通常使用单调队列，但是具体实现采用双端队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int[] resultArr = new int[nums.length - (k - 1)];
        Deque<Integer> deque = new LinkedList<>();
        for (int i = 0, j = 1 - k; i < nums.length; i++, j++) {
            // 如果被删除的值正好是之前窗口中最大的元素，则需要在队列中移除。
            // 保证队列中的元素都在窗口中
            if (j > 0 && deque.getFirst() == nums[j - 1]) {
                deque.removeFirst();
            }
            // 从队列尾部加入元素，加入前判断队列尾部的值是否小于要加入的值，小于则删除
            while (deque.size() != 0 && deque.getLast() < nums[i]) {
                deque.removeLast();
            }
            deque.addLast(nums[i]);
            if (j >= 0) {
                resultArr[j] = deque.getFirst();
            }
        }
        return resultArr;
    }
}

另一种写法，队列中保存的是窗口中元素的下标，通过下标判断元素是否在窗口中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int[] resultArr = new int[nums.length - (k - 1)];
        Deque<Integer> deque = new LinkedList<>();
        for (int i = 0, j = 1 - k; i < nums.length; i++, j++) {
            if (j > 0 && deque.getFirst() < j) {
                deque.removeFirst();
            }
            while (deque.size() != 0 && nums[deque.getLast()] < nums[i]) {
                deque.removeLast();
            }
            deque.addLast(i);
            if (j >= 0) {
                resultArr[j] = nums[deque.getFirst()];
            }
        }
        return resultArr;
    }
}

最小覆盖子串

https://leetcode.cn/problems/minimum-window-substring/description/?envType=study-plan-v2&envId=top-100-liked
使用滑动窗口，窗口由两个指针控制大小，右指针负责扩大窗口，左指针负责收缩窗口。如果当前窗口不覆盖子串，则扩大窗口，如果覆盖子串，则收缩窗口更新结果，直至不能收缩。

❓问题在于如何判断是否覆盖？

可以使用哈希表存储窗口中每个字符出现的次数，如果目标字符串中的字符出现的次数都小于等于窗口中的，则说明覆盖，否则不覆盖。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public String minWindow(String s, String t) {
        char[] chsArr = s.toCharArray();
        char[] chtArr = t.toCharArray();
        Map<Character, Integer> chCntMp = new HashMap<>();
        for (char ch : chtArr) {
            chCntMp.put(ch, chCntMp.getOrDefault(ch, 0) + 1);
        }
        Map<Character, Integer> winMap = new HashMap<>();
        int ansLeft = -1, ansRight = chsArr.length;
        for (int i = 0, j = 0; i < chsArr.length; i++) {
            winMap.put(chsArr[i], winMap.getOrDefault(chsArr[i], 0) + 1);
            while (isCover(winMap, chCntMp)) {
                if (i - j + 1 < ansRight - ansLeft + 1) {
                    ansRight = i;
                    ansLeft = j;
                }
                winMap.put(chsArr[j], winMap.get(chsArr[j++]) - 1);
            }
        }
        return ansLeft == -1 ? "" : s.substring(ansLeft, ansRight + 1);
    }

    public boolean isCover(Map<Character, Integer> s, Map<Character, Integer> t) {
        if (s.size() < t.size()) {
            return false;
        }
        for (Map.Entry<Character, Integer> entry : t.entrySet()) {
            if (s.getOrDefault(entry.getKey(), 0) < entry.getValue()) {
                return false;
            }
        }
        return true;
    }
}

最大子数组和

https://leetcode.cn/problems/maximum-subarray/?envType=study-plan-v2&envId=top-100-liked
利用动态规划可以达到O(N)的时间复杂度。
假定dp[i]表示以第 i 个数结尾的最大的子数组的和，所以递归公式：dp[i] = max(dp[i - 1] + nums[i], nums[i])，如果前一个子数组加上nums[i]数组和变小，就认为最大的数组是nums[i]自己。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int maxSubArray(int[] nums) {
        int ans = Integer.MIN_VALUE;
        for (int i = 0; i < nums.length; i++) {
            if (i > 0) {
                nums[i] = Math.max(nums[i], nums[i - 1] + nums[i]);
            }
            ans = Math.max(ans, nums[i]);
        }
        return ans;
    }
}

轮转数组

https://leetcode.cn/problems/rotate-array/?envType=study-plan-v2&envId=top-100-liked
主要是空间复杂度达到O(1)，不适用额外的数组。
可以采用基于交换的方式，通过观察结果，可以发现，向右移动 k 个单位后，后边 k 个数移动到前 k 个位置，其余的移动到了后 k 个位置。如果先采用整体翻转的方式，可以将后 k 的数移动到前 k 个位置，但是顺序和正确的顺序相反，因此再对局部进行依次翻转即可。
❗ 这里有一个需要注意：如果轮转的长度 k，大于数组长度，可以采用一次取模操作，当 k 和数组长度相等时，轮转后和原数组相同，所以可以认为 k 取模后的结果为真实的需要轮转的长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public void rotate(int[] nums, int k) {
        k %= nums.length;
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.length - 1);
    }

    private void reverse(int[] nums, int start, int end) {
        for (int i = start, j = end; i < j; i++, j--) {
            int temp = nums[i];
            nums[i] = nums[j];
            nums[j] = temp;
        }
    }
}

缺失的第一个正数

41. 缺失的第一个正数 - 力扣（LeetCode）

难点在于不能使用额外空间。如果可以使用额外空间，可以使用哈希表，存储每一个元素，然后从 1 开始遍历，直到发现不存在于哈希表中的值即可。

如果要降低空间复杂度，可以考虑原地哈希。

通过观察结果，会发现，结果肯定存在于[1, n+1]中，n 为数组长度，如果数组中的数在[1, n]都存在，则说明结果为 n + 1，否则为[1, n]中不存在的最小的数，这里可以使用原地哈希，具体方法可以采用标记法，遍历数组，如果 nums[i]范围在[1, n]中，则给 nums[nums[i] - 1]打上标记，这里打标记可以设置为负数，因为原数组中存在负数，可以令原来的负数设为一个不可能的值，如 n + 1 或者更大，这样所有数都是正数了。当遍历完所有打完标记，如果所有的数都是负数了，说明都存在了，否则为第一个不为负数的下标+ 1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int firstMissingPositive(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] <= 0) {
                nums[i] = nums.length + 1;
            }
        }
        for (int i = 0; i < nums.length; i++) {
            int temp = Math.abs(nums[i]);
            if (temp >= 1 && temp <= nums.length) {
                nums[temp - 1] = -Math.abs(nums[temp - 1]);
            }
        }
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] > 0) {
                return i + 1;
            }
        }
        return nums.length + 1;
    }
}

旋转图像

48. 旋转图像 - 力扣（LeetCode）
通过观察例子中的旋转，固定的位置之间会形成一个完整的旋转链，因此可以使用原地操作数据，不需要使用新的二维数组。

所以接下来的重点是寻找旋转链之间的对应的坐标关系。以左上角的(i, j)为例，

旋转一次后的坐标为：(j, n - i - 1)，可以理解为，(i, j)所在的列变成了行，行变成了列。从行看，i行的数据会变成列，行是从上往下数，那么变成列后就是从右往左数，所以列就是n - i - 1。从列看，从左向右看，变成行就是从上往下看，因此就是j。

(j, n - i - 1)再旋转一次后，坐标为：(n - i - 1, n - j - 1)，从行看，是从上往下，旋转后的列则是从右向左，所以是n - j - 1。从列看，从右往左，旋转后的行则是从下往上，n - i - 1

依此类推：(n - j - 1, i)

最后的坐标旋转链(i, j) -> (j, n - i - 1) -> (n - i - 1, n - j - 1) -> (n - j - 1, i) -> (i, j)

因此，原地操作只需要按照这个顺序依次赋值即可。

接下来需要考虑的是，遍历哪些数据进行旋转操作。只有两种情况，n 为奇数和偶数的情况。

n 为偶数：只需要考虑左上角 行[0, n / 2) 列[0, n / 2)的情况

n 为奇数：不需要考虑正中心的数，然后需要旋转的则是正中心左方和上方组成的区域，即 行[0, n / 2) 列[0, n / 2]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < (n + 1) / 2; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - 1 - j][i];
                matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
                matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
                matrix[j][n - 1 - i] = temp;
            }
        }
    }
}

相交链表

160. 相交链表 - 力扣（LeetCode）

判断两个链表是否相交，可以使用双指针的方式，题目中保证链表中不存在环，因此大大简化了判断条件。

两个指针分别遍历两个链表，当遍历到末尾时再遍历另一个链表，直到指向相同的节点，即为相交的第一个节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        return getIntersectionNode(headA, headB, null);
    }

    private ListNode getIntersectionNode(ListNode headA, ListNode headB, ListNode endNode) {
        if (headA == null || headB == null) {
            return null;
        }
        ListNode pA = headA;
        ListNode pB = headB;
        while (pA != pB) {
            pA = pA == endNode ? headB : pA.next;
            pB = pB == endNode ? headA : pB.next;
        }
        return pA;
    }
}

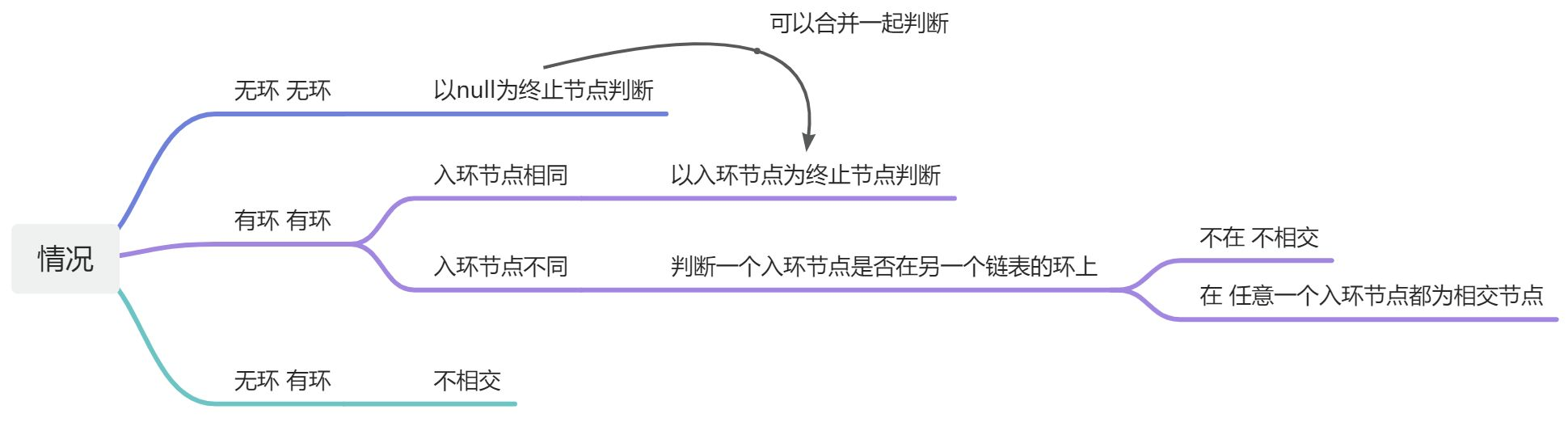
❓ 如果链表中存在环呢？则需要考虑多种情况。

这里认为链表都是单链表

  1. 情况 1：两个链表都无环双指针，遍历链表 A 和 B，当指针为 null 时从另一个节点的头节点开始遍历。直到两个指针相等（两个指针相等时，如果为 null 则表示没有相交节点，否则有相交节点）面试题 02.07. 链表相交 - 力扣（LeetCode）
1
2
3
4
5
6
7
8
9
10
11
12
13
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) {
            return null;
        }
        ListNode pA = headA, pB = headB;
        while (pA != pB) {
            pA = pA == null ? headB : pA.next;
            pB = pB == null ? headA : pB.next;
        }
        return pA;
    }
}

❗注意：判断是否为null时，使用的是pA当前指针，而不是pA.next，如果使用pA.next来判断，当不相交时，会发生无限循环的情况，pA和pB会一直不相等（也不为null)。所以使用pA当前指针。可以理解为，把最后链表结束时指向的null指针也算作一个节点，然后两个链表不相交时，最后都会指向null节点，那么两个链表就在null节点“相交”了，如下图所示。

  1. 情况 2：一个有环一个无环（一定不相交）如果相交，则肯定有一个节点有两个next指针，这不满足单链表。所以一定不相交。
  2. 情况 3：两个都有环
    • 不相交
    • 在非环处相交
    • 在环处相交

相交只有两种情况

找到两个带环链表的入环节点，然后固定一个，遍历另一个，直到能找到一个节点和固定节点相等，则证明相交，否则不相交。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// circleNode1 circleNode2是两个节点的入环节点

// 如果入环节点相同，说明必然是情况1。否则是情况2或者不相交
if (circleNode1 == circleNode2) {
    // 利用circleNode1或者2为末尾节点，利用无环链表求相交节点方式求相交的节点。
    return true;
}
Node temp = circleNode2.next;
while(temp != circleNode2) {
    if(temp == circleNode1)
        // circleNode1 或者  circleNode2为相交节点都可以
        return true;
    temp = temp.next;
}
// 不相交
return false;

所以所有情况如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public static ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    ListNode cycleNodeA = hasCycle(headA);
    ListNode cycleNodeB = hasCycle(headB);
    if (cycleNodeA == cycleNodeB) {
        // 说明两个都是无环的，直接判断是否相交
        // if (cycleNodeA == null) {
        //     return getIntersectionNodeNoLoop(headA, headB, null);
        // }
        // 否则是都有环，入环节点相同，必然相交，以入环节点为终止节点求相交节点
        // return getIntersectionNodeNoLoop(headA, headB, cycleNodeA);
        // 以上代码可以直接合并为下面一行
        return getIntersectionNodeNoLoop(headA, headB, cycleNodeA);
    }
    // 说明两个入环节点不相等，要么有一个为空，要么都不为空，如果有一个为空，则表示肯定不相交
    if (cycleNodeA == null || cycleNodeB == null) {
        return null;
    }
    // 如果环上相交，说明从一个入环节点开始遍历，一定能到达另一个入环节点
    ListNode temp = cycleNodeA;
    while (temp != cycleNodeB) {
        temp = temp.next;
        // 转了一圈发现回到原位置了，说明没有相交
        if (temp == cycleNodeA) {
            return null;
        }
    }
    // 相交，任意一个入环节点都可以是相交节点。
    return cycleNodeA;
    // 如果入环节点不同，并且相交，那么肯定有两个相交节点
    // return cycleNodeB;
}
// 判断一个链表是否有环
public static ListNode hasCycle(ListNode head) {
    if (head == null) {
        return null;
    }
    ListNode slow = head, fast = head;
    while (fast.next != null && fast.next.next != null) {
        slow = slow.next;
        fast = fast.next.next;
        if (fast == slow) {
            fast = head;
            while (fast != slow) {
                fast = fast.next;
                slow = slow.next;
            }
            return fast;
        }
    }
    return null;
}
// 判断两个无环链表是否相交，手动设定终止节点endNode
public static ListNode getIntersectionNodeNoLoop(ListNode headA, ListNode headB, ListNode endNode) {
    ListNode pA = headA, pB = headB;
    while (pA != pB) {
        pA = pA == endNode ? headB : pA.next;
        pB = pB == endNode ? headA : pB.next;
    }
    return pA;
}

反转链表

206. 反转链表 - 力扣（LeetCode）

使用三个指针分别指向“上一个节点”“当前节点”和“下一个节点”，遍历过程中反转“上一个节点”和“当前节点”的指向。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre = null, cur = head;
        while (cur != null) {
            ListNode next = cur.next;
            cur.next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }
}

回文链表

234. 回文链表 - 力扣（LeetCode）

需要使用O(1)的空间复杂度，回文的定义：从前向后和从后向前遍历的结果相同。但是原链表是单向链表，因此如果想从后向前遍历，需要将后半部分的链表反转。

因此需要判断什么时候到达了“中间”位置，然后将中间及其之后的链表反转。

这里使用快慢指针，因为快指针行进速度是慢指针 2 倍，所以当快指针到结尾时，慢指针行进了链表长度的一半。

这里分两种情况考虑，链表长度为奇数和偶数。

如图所示，当快慢指针结束时，奇数长度的链表慢指针在正中心的位置，偶数长度的链表慢指针在前半部分的最后一个节点位置。

通过观察可以知道，奇数长度的链表正中心的节点并不影响整体的回文性，偶数长度的链表需要将后半部分的链表反转，因此可以确定需要反转的链表的头节点为slow.next，反转完后返回右半部分头节点，从左半部分头节点和右半部分头节点同时遍历，如果不同则直接返回false，需要注意终止条件是右半部分的节点走到null，因为链表长度为奇数时，左半部分的链表会多一个中心节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public boolean isPalindrome(ListNode head) {
        if (head == null) {
            return true;
        }
        ListNode fast = head, slow = head;
        while (fast.next != null && fast.next.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        fast = reverse(slow.next);
        // 保存反转后的链表的头节点
        ListNode temp = fast;
        slow = head;
        while (fast != null) {
            if (fast.val != slow.val) {
                return false;
            }
            fast = fast.next;
            slow = slow.next;
        }
        // 链表恢复原状
        reverse(temp);
        return true;
    }

    private ListNode reverse(ListNode head) {
        ListNode pre = null, cur = head;
        while (cur != null) {
            ListNode next = cur.next;
            cur.next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }
}

环形链表

142. 环形链表 II - 力扣（LeetCode）

判断链表是否有环，使用快慢指针，当快慢指针相遇时表明存在环，然后将快指针从头节点开始遍历，每次移动一个位置，直到再次相遇的节点即为环形的入口。

❓ 为什么将快指针从头节点开始遍历就能找到入口？下边给出证明：

假设环形链表中三个点，头节点 A，入口节点 B，快慢指针相遇的节点 C。因为快指针的速度是慢指针的 2 倍，所以快指针行进的距离是慢指针的 2 倍，所以有image，移项可得image即image，也就是说从 C 点和 A 点出发，以同样的速度行进，会同时到达 B 即入口节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null) {
            return null;
        }
        ListNode slow = head, fast = head;
        while (fast.next != null && fast.next.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                fast = head;
                while (slow != fast) {
                    slow = slow.next;
                    fast = fast.next;
                }
                return fast;
            }
        }
        return null;
    }
}

删除链表的倒数第 N 个节点

19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode）

要求使用一趟遍历，难点在于遍历一趟就要找到第 N 个节点所在的位置。如果只用一个指针遍历长度，则需要遍历两次。

如果使用两个指针，让第一个指针先走n - 1步，然后让第二个指针和第一个指针同时行进，则可以保证两个指针的距离固定，当第一个指针到达结尾时，第二个指针的位置则为需要删除的节点，然后进行删除即可。（注意：需要多一个pre指针，不然无法删除）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode first = head;
        ListNode second = head;
        ListNode pre = null;
        for (int i = 0; i < n - 1; i++) {
            first = first.next;
        }
        while (first.next != null) {
            first = first.next;
            pre = second;
            second = second.next;
        }
        if (pre == null) {
            return head.next;
        }
        pre.next = second.next;
        return head;
    }
}

两两交换链表中的节点

24. 两两交换链表中的节点 - 力扣（LeetCode）

采用“类似头插法”方式，设置一个temp节点，temp节点指向的后续的节点即为需要交换的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode ansHead = new ListNode();
        // 保证temp的后续节点存在
        ansHead.next = head;
        ListNode temp = ansHead;
        // 保证后续节点存在两个节点才可以交换，否则不能交换
        while (temp.next != null && temp.next.next != null) {
            ListNode node1 = temp.next;
            ListNode node2 = temp.next.next;
            temp.next = node2;
            // 保证链表使用是连接的，没有断开
            node1.next = node2.next;
            node2.next = node1;
            // 进行xi
            temp = node1;
        }
        return ansHead.next;
    }
}

K 个一组翻转链表

25. K 个一组翻转链表 - 力扣（LeetCode）

要求 K 个一组，可以参考删除链表的倒数第 N 个节点，先走 K 步，然后翻转这 K 个链表，依此类推。

需要注意的是设置一个dummy节点，即带头节点，方便后续操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} k
 * @return {ListNode}
 */
var reverseKGroup = function (head, k) {
  let dummy = new ListNode(0, head);
  let pre = dummy,
    cur = dummy;
  while (cur.next !== null) {
    for (let i = 0; i < k && cur; i++) {
      cur = cur.next;
    }
    if (!cur) {
      break;
    }
    let start = pre.next,
      end = cur.next;
    pre.next = reverse(start, end);
    start.next = end;
    pre = start;
    cur = start;
  }
  return dummy.next;
};
/**
  head为头节点，end为最后一个节点的下一个节点（理解为null）
*/
function reverse(head, end) {
  if (!head) {
    return null;
  }
  let pre = null,
    cur = head;
  while (cur !== end) {
    let next = cur.next;
    cur.next = pre;
    pre = cur;
    cur = next;
  }
  return pre;
}

随机链表的复制

138. 随机链表的复制 - 力扣（LeetCode）

方法一：哈希表，存储每个节点的对应复制的节点，然后遍历添加指针。

方法二： 构造新链表旧链表1 -> 新链表1 -> 旧链表2 -> 新链表2 -> ... -> 旧链表n -> 新链表n，然后遍历，通过旧链表的random指针，找到新链表的random节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * // Definition for a _Node.
 * function _Node(val, next, random) {
 *    this.val = val;
 *    this.next = next;
 *    this.random = random;
 * };
 */

/**
 * @param {_Node} head
 * @return {_Node}
 */
var copyRandomList = function (head) {
  if (!head) {
    return null;
  }
  // 复制链表
  let temp = head;
  while (temp) {
    let node = new _Node(temp.val, temp.next, null);
    temp.next = node;
    temp = node.next;
  }
  // 连接新节点的random指针
  temp = head;
  while (temp) {
    if (temp.random) {
      temp.next.random = temp.random.next;
    }
    temp = temp.next.next;
  }
  // 拆分链表
  temp = head;
  let ansHead = head.next;
  let ansTemp = ansHead;
  while (temp) {
    temp.next = ansTemp.next;
    temp = ansTemp.next;
    if (temp) {
      ansTemp.next = temp.next;
      ansTemp = temp.next;
    }
  }
  return ansHead;
};

排序链表

148. 排序链表 - 力扣（LeetCode）

链表排序，通常使用归并排序。

利用快慢指针找到中点，然后两边分别排序、归并。

注意的是 ?? 和 || 的区别：

  • x ?? y是当x为null、undefined时取 y，如果x为false、0、''这种仍然取x。
  • x || y当x为假值即null、undefined、false、0、''这些值时取y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var sortList = function (head) {
  if (!head || !head.next) {
    return head;
  }
  let fast = head,
    slow = head;
  while (fast.next && fast.next.next) {
    fast = fast.next.next;
    slow = slow.next;
  }
  let mid = slow.next;
  slow.next = null;
  let left = sortList(head);
  let right = sortList(mid);
  let ansHead = new ListNode();
  let tail = ansHead;
  while (left && right) {
    if (left.val < right.val) {
      tail.next = left;
      left = left.next;
    } else {
      tail.next = right;
      right = right.next;
    }
    tail = tail.next;
  }

  tail.next = left ?? right;
  return ansHead.next;
};

合并 K 个升序链表

23. 合并 K 个升序链表 - 力扣（LeetCode）

归并排序的思想，每两个合成一个，然后继续合成，直到剩下最后一个。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode[]} lists
 * @return {ListNode}
 */
var mergeKLists = function (lists) {
  if (lists.length === 0) {
    return null;
  }
  return mergeList(lists, 0, lists.length - 1);
};

function mergeList(lists, left, right) {
  if (left >= right) {
    return lists[left];
  }
  let mid = (left + right) >> 1;
  let leftList = mergeList(lists, left, mid);
  let rightList = mergeList(lists, mid + 1, right);
  let dummy = new ListNode();
  let tail = dummy;
  while (leftList && rightList) {
    if (leftList.val < rightList.val) {
      tail.next = leftList;
      leftList = leftList.next;
    } else {
      tail.next = rightList;
      rightList = rightList.next;
    }
    tail = tail.next;
  }
  tail.next = leftList ?? rightList;
  return dummy.next;
}

实现 LRU 缓存

146. LRU 缓存 - 力扣（LeetCode）

最近最少使用缓存，可以使用一个链表保存数据，如果被使用了则放在链表头或者尾，这样一来，链表的某个方向上就是最近的使用频率递减的趋势。同时使用链表移动数据的操作是 O(1)的。

但是查找很耗时，因此可以采用哈希的方式，存储每个 key 对应的链表的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
class ListNode {
  constructor(val, pre, next) {
    this.val = val ?? { key: 0, value: 0 };
    this.pre = pre ?? null;
    this.next = next ?? null;
  }
}

/**
 * @param {number} capacity
 */
var LRUCache = function (capacity) {
  this.capacity = capacity;
  this.size = 0;
  this.dummyHead = new ListNode();
  this.dummyTail = new ListNode();
  this.dummyHead.next = this.dummyTail;
  this.dummyTail.pre = this.dummyHead;
  this.kv = new Map();
};

/**
 * @param {number} key
 * @return {number}
 */
LRUCache.prototype.get = function (key) {
  if (!this.kv.has(key)) {
    return -1;
  }
  const temp = this.kv.get(key);
  removeNode(temp);
  addToTail(this.dummyTail, temp);
  return temp.val.value;
};

/**
 * @param {number} key
 * @param {number} value
 * @return {void}
 */
LRUCache.prototype.put = function (key, value) {
  if (this.kv.has(key)) {
    const temp = this.kv.get(key);
    temp.val.value = value;
    removeNode(temp);
    addToTail(this.dummyTail, temp);
  } else {
    const temp = new ListNode({ key, value });
    addToTail(this.dummyTail, temp);
    this.kv.set(key, temp);
    if (this.size < this.capacity) {
      this.size++;
    } else {
      this.kv.delete(this.dummyHead.next.val.key);
      removeNode(this.dummyHead.next);
    }
  }
};

function removeNode(temp) {
  temp.pre.next = temp.next;
  temp.next.pre = temp.pre;
}

function addToTail(dummyTail, temp) {
  temp.next = dummyTail;
  temp.pre = dummyTail.pre;
  dummyTail.pre = temp;
  temp.pre.next = temp;
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * var obj = new LRUCache(capacity)
 * var param_1 = obj.get(key)
 * obj.put(key,value)
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
struct Node {
    int key, val;
    Node *next;
    Node *prev;
    Node(int key, int val) {
        this->key = key;
        this->val = val;
        this->next = nullptr;
        this->prev = nullptr;
    }
    Node(int key, int val, Node *next, Node *prev) {
        this->key = key;
        this->val = val;
        this->next = next;
        this->prev = prev;
    }
};
class LRUCache {
public:
    int size;
    unordered_map<int, Node*> hash;
    Node *dummyHead;
    Node *dummyTail;
    LRUCache(int capacity) {
        size = capacity;
        dummyHead = new Node(0, 0);
        dummyTail = new Node(0, 0);
        dummyHead->next = dummyTail;
        dummyTail->prev = dummyHead;
    }

    void addNodeToHead(Node *temp) {
        temp->next = dummyHead->next;
        temp->prev = dummyHead;
        dummyHead->next->prev = temp;
        dummyHead->next = temp;
    }

    void removeNode(Node *temp) {
        temp->prev->next = temp->next;
        temp->next->prev = temp->prev;
    }

    int get(int key) {
        if (!hash.count(key)) {
            return -1;
        }
        auto temp = hash[key];
        removeNode(temp);
        addNodeToHead(temp);
        return temp->val;
    }

    void put(int key, int value) {
        if (hash.count(key)) {
            auto temp = hash[key];
            temp->val = value;
            removeNode(temp);
            addNodeToHead(temp);
        } else {
            auto temp = new Node(key, value);
            hash[key] = temp;
            addNodeToHead(temp);
            if (hash.size() > size) {
                auto removed = dummyTail->prev;
                removeNode(removed);
                hash.erase(removed->key);
                delete removed;
            }
        }
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

二叉树的层序遍历

102. 二叉树的层序遍历 - 力扣（LeetCode）

层序遍历使用队列即可，但是题目中要求每一层的数据单独作为一个子数组保存。

在每次遍历队列之前，可以获取队列的长度，即表示当前层的节点个数。然后一次性遍历当前层所有的节点，下一次遍历的时候，就是遍历的下一层的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function (root) {
  if (!root) {
    return [];
  }
  const ans = [];
  const que = [root];
  while (que.length) {
    const ret = [];
    const size = que.length;
    for (let i = 0; i < size; i++) {
      const temp = que.shift();
      ret.push(temp.val);
      if (temp.left) {
        que.push(temp.left);
      }
      if (temp.right) {
        que.push(temp.right);
      }
    }
    ans.push(ret);
  }
  return ans;
};

将有序数组转为平衡二叉搜索树

108. 将有序数组转换为二叉搜索树 - 力扣（LeetCode）

要求为平衡二叉树，利用二分查找得到的搜索树是平衡的，可以利用二分查找的思路构造。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var sortedArrayToBST = function (nums) {
  return recur(nums, 0, nums.length - 1);
};

function recur(nums, left, right) {
  if (left === right) {
    return new TreeNode(nums[left]);
  } else if (left > right) {
    return null;
  }
  const mid = (left + right) >> 1;
  const root = new TreeNode(nums[mid]);
  root.left = recur(nums, left, mid - 1);
  root.right = recur(nums, mid + 1, right);
  return root;
}

验证是否是二叉搜索树

98. 验证二叉搜索树 - 力扣（LeetCode）

利用二叉搜索树的性质，中序遍历的结果是有序的。因此可以采用中序遍历，同时使用一个变量保存遍历时上次的结果，当前值大于上一次的值并且左右子树都为二叉搜索树才为二叉搜索树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function (root) {
  let pre = Number.MIN_SAFE_INTEGER;
  function recur(root) {
    if (!root) {
      return true;
    }
    const leftBST = recur(root.left);
    const cur = root.val;
    if (pre < cur) {
      pre = cur;
    } else {
      return false;
    }
    const rightBST = recur(root.right);
    return leftBST && rightBST;
  }
  return recur(root);
};

二叉搜索树第 K 小的元素

230. 二叉搜索树中第 K 小的元素 - 力扣（LeetCode）

由二叉搜索树的性质，中序遍历为从小到大的序列，可以采用中序遍历的方式，遍历到第 K 个数的时候记录值，即为第 K 小的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var kthSmallest = function (root, k) {
  let ans = 0;
  function recur(root) {
    if (!root) {
      return;
    }
    recur(root.left);
    // 遍历一个之后k减1，当k === 0时说明已经遍历到了，后续就不能再遍历了。
    if (k === 0) {
      return;
    }
    if (k === 1) {
      ans = root.val;
    }
    k--;
    recur(root.right);
  }
  recur(root);
  return ans;
};

二叉树的右视图

199. 二叉树的右视图 - 力扣（LeetCode）

要求每一层的最右边的数据，可以考虑用层序遍历，每一层的最后一个数据为结果集的数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var rightSideView = function (root) {
  if (!root) {
    return [];
  }
  const ans = [];
  const que = [];
  que.push(root);
  while (que.length) {
    const size = que.length;
    for (let i = 0; i < size; i++) {
      const temp = que.shift();
      if (i === size - 1) {
        ans.push(temp.val);
      }
      // 下边两个判断可以用另一种方式写
      // temp.left && que.push(temp.left)
      // temp.right && que.push(temp.right)
      if (temp.left) {
        que.push(temp.left);
      }
      if (temp.right) {
        que.push(temp.right);
      }
    }
  }
  return ans;
};

二叉树展开为链表

114. 二叉树展开为链表 - 力扣（LeetCode）

按照先序遍历方式展开，左指针始终为 null，而元素都在右指针，考虑按照递归的做法，将左右子树分别展开，然后将左子树的节点（如果有）链接到右子树上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var flatten = function (root) {
  if (!root) {
    return null;
  }
  flatten(root.left);
  flatten(root.right);
  let temp = root.left;
  if (temp) {
    // 一直找到展开好的左子树的最后的节点
    while (temp.right) {
      temp = temp.right;
    }
    temp.right = root.right;
    root.right = root.left;
    root.left = null;
  }
};

要求使用O(1)的空间复杂度，不使用前序遍历的方式，转换思路。

前序遍历特点为：根、左、右，如果要展开成一个链表，则当前节点curr的右子节点，一定排在curr的左子树的某个节点之后。根据特点，可以知道，左子树的最后一个节点一定是左子树（非空）最右侧的节点，因此找到后，可以认为这个最右侧的节点是当前节点的右子节点的前驱结点prev，将prev的右孩子设置为当前节点的右子节点，将当前节点的左子树设置为右孩子（因为左子树一定是当前节点的后驱节点），并将左子树置空。将当前节点向右孩子走一步，完成一轮循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        if (!root) return;
        auto curr = root;
        while (curr) {
            if (curr->left) {
                auto prev = curr->left;
                while (prev->right) {
                    prev = prev->right;
                }
                prev->right = curr->right;
                curr->right = curr->left;
                curr->left = nullptr;
            }
            curr = curr->right;
        }
    }
};

从前序遍历和中序遍历构造二叉树

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

根据前序遍历特点，最先遍历的肯定是根节点，所以第一个数一定是根节点，然后根据这个根节点，从中序遍历找到对应的位置，那么中序遍历该位置的左边为左子树的节点，右边为右子树的节点，依次递归。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function (preorder, inorder) {
  function recur(preorder, preLeft, preRight, inorder, inLeft, inRight) {
    if (preLeft > preRight) {
      return null;
    }
    const root = new TreeNode(preorder[preLeft]);
    const inIndex = inorder.findIndex((item) => item === root.val);
    const leftLength = inIndex - inLeft,
      rightLength = inRight - inIndex;
    root.left = recur(
      preorder,
      preLeft + 1,
      preLeft + leftLength,
      inorder,
      inLeft,
      inIndex - 1
    );
    root.right = recur(
      preorder,
      preLeft + leftLength + 1,
      preRight,
      inorder,
      inIndex + 1,
      inRight
    );
    return root;
  }
  return recur(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
};

路径总和 Ⅲ

437. 路径总和 III - 力扣（LeetCode）

法一：深度优先搜索，每次计算以root为根节点，向下计算满足targetSum的个数，记为rootSum(root, targetSum)，然后递归遍历每个节点，计算以每个节点为根节点的满足条件的个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function (root, targetSum) {
  if (!root) {
    return 0;
  }
  return (
    rootSum(root, targetSum) +
    pathSum(root.left, targetSum) +
    pathSum(root.right, targetSum)
  );
};

function rootSum(root, targetSum) {
  if (!root) {
    return 0;
  }
  return (
    rootSum(root.left, targetSum - root.val) +
    rootSum(root.right, targetSum - root.val) +
    (root.val === targetSum ? 1 : 0)
  );
}

法二：前缀和

从root节点到node节点的路径上的和记为前缀和，可以看作是一维的前缀和。

使用前序遍历，遍历过程中记录前缀和，同时记录满足该前缀和的节点个数。

如果root到node之间的节点p满足prefixSum - targetSum，则说明p节点的下一个节点到node节点前缀和为targetSum。

计算完成后恢复，因为计算其他路径的前缀和时可能有相同的前缀和，但是其他路径的会影响当前路径，因此需要删除。参考：题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function (root, targetSum) {
  if (!root) {
    return 0;
  }
  const prefix = new Map();
  prefix.set(0, 1);
  return dfs(root, prefix, 0, targetSum);
};

function dfs(root, prefix, curr, targetSum) {
  if (!root) {
    return 0;
  }
  curr += root.val;
  let ret = prefix.get(curr - targetSum) ?? 0;
  prefix.set(curr, (prefix.get(curr) ?? 0) + 1);
  ret += dfs(root.left, prefix, curr, targetSum);
  ret += dfs(root.right, prefix, curr, targetSum);
  prefix.set(curr, prefix.get(curr) - 1);
  return ret;
}

二叉树的最近公共祖先

236. 二叉树的最近公共祖先 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function (root, p, q) {
  if (!root || root === p || root === q) {
    return root;
  }
  const left = lowestCommonAncestor(root.left, p, q);
  const right = lowestCommonAncestor(root.right, p, q);
  if (!left) {
    return right;
  }
  if (!right) {
    return left;
  }
  return root;
};

二叉树中的最大路径和

124. 二叉树中的最大路径和 - 力扣（LeetCode）

采用递归的方式，设置maxGain(root)函数，表示从从root节点上能获得的最大贡献值，贡献值表示为从root节点向左子树或者右子树延申（只能是root的左子树或者右子树一个方向），得到的最大的值，以此类推，roo.left的最大贡献值表示为root.left向左子树或者右子树延申。这是一个递归的过程。

可以在递归的时候求出最大的路径和。当左子树和右子树的最大贡献值大于 0 的时候，才能算作贡献去计算路径和，否则还不如直接使用根节点当作单独的路径和大。最后返回贡献值，选择左右子树最大的作为贡献值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxPathSum = function (root) {
  let maxSum = -Infinity;
  function maxGain(root) {
    if (!root) {
      return 0;
    }
    const leftGain = Math.max(maxGain(root.left), 0);
    const rightGain = Math.max(maxGain(root.right), 0);
    const temp = root.val + leftGain + rightGain;
    console.log(maxSum);
    maxSum = Math.max(maxSum, temp);
    return root.val + Math.max(leftGain, rightGain);
  }
  maxGain(root);
  return maxSum;
};

岛屿数量

200. 岛屿数量 - 力扣（LeetCode）

使用深度优先遍历，遇到1后进行深度优先遍历，将遍历到的所有1进行标记，组成岛屿。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * @param {character[][]} grid
 * @return {number}
 */
var numIslands = function (grid) {
  const m = grid.length,
    n = grid[0].length;
  const visited = new Array(m).fill(null).map((item) => new Array(n).fill(false));
  const dx = [0, 1, 0, -1],
    dy = [1, 0, -1, 0];
  function dfs(grid, x, y) {
    visited[x][y] = true;
    for (let i = 0; i < dx.length; i++) {
      const nx = x + dx[i],
        ny = y + dy[i];
      if (
        nx < 0 ||
        ny < 0 ||
        nx >= m ||
        ny >= n ||
        grid[nx][ny] === '0' ||
        visited[nx][ny]
      ) {
        continue;
      }
      dfs(grid, nx, ny);
    }
  }

  let ans = 0;
  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[i].length; j++) {
      // 遍历每一个元素，当为1且没有被访问时，说明会组成一个新的岛屿，结果+1
      if (grid[i][j] === '1' && !visited[i][j]) {
        dfs(grid, i, j);
        ans++;
      }
    }
  }
  return ans;
};

腐烂的橘子

994. 腐烂的橘子 - 力扣（LeetCode）

多源的宽度优先搜索，因为可能同时存在多个腐烂的橘子，是同时扩散的。

初始时找到所有腐烂的橘子加入队列，作为初始的多个起点，然后遍历，同时这里使用了102. 二叉树的层序遍历 - 力扣（LeetCode）的方法，每一次遍历“一层”。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * @param {number[][]} grid
 * @return {number}
 */
var orangesRotting = function (grid) {
  const m = grid.length,
    n = grid[0].length;
  const que = [];
  // 保存所有好的橘子
  let cnt = 0;
  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[i].length; j++) {
      grid[i][j] === 2 && que.push([i, j]);
      grid[i][j] === 1 && cnt++;
    }
  }
  const dx = [0, 1, 0, -1],
    dy = [1, 0, -1, 0];
  let ans = 0;
  // 没有遍历完并且还有好的橘子，说明可以继续腐烂，否则，不再继续遍历。
  while (que.length && cnt) {
    ans++;
    let size = que.length;
    while (size--) {
      const [x, y] = que.shift();
      for (let i = 0; i < dx.length; i++) {
        const nx = x + dx[i],
          ny = y + dy[i];
        if (nx < 0 || ny < 0 || nx >= m || ny >= n || grid[nx][ny] !== 1) {
          continue;
        }
        // 腐烂后则减1
        cnt--;
        grid[nx][ny] = 2;
        que.push([nx, ny]);
      }
    }
  }
  // 如果还有好的橘子，说明不可能
  return cnt === 0 ? ans : -1;
};

课程表

207. 课程表 - 力扣（LeetCode）

拓扑排序，首先是图的构造，使用二维数组表示，graph[i] = [a, b, c]表示i指向a, b, c。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * @param {number} numCourses
 * @param {number[][]} prerequisites
 * @return {boolean}
 */
var canFinish = function (numCourses, prerequisites) {
  const graph = new Array(numCourses).fill(null).map((item) => []);
  const indegree = new Array(numCourses).fill(0);
  for (const [a, b] of prerequisites) {
    graph[b].push(a);
    indegree[a]++;
  }
  const que = [];
  for (let i = 0; i < numCourses; i++) {
    indegree[i] === 0 && que.push(i);
  }
  while (que.length) {
    const i = que.shift();
    for (const j of graph[i]) {
      indegree[j]--;
      indegree[j] === 0 && que.push(j);
    }
  }
  for (let i = 0; i < numCourses; i++) {
    if (indegree[i] !== 0) {
      return false;
    }
  }
  return true;
};

实现 Trie 树

208. 实现 Trie (前缀树) - 力扣（LeetCode）

每个节点（假设）有 26 个子树（根据字符集决定），每个边表示一个字符，如果有这个边，表示存在，没有边表示不存在。

如果需要判断每个单词出现了多少次，或者是以某个单词为前缀的单词有多少个，可以增加变量 end: int, pass: int用数量表示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
var Trie = function () {
  this.next = new Map();
  this.end = false;
};

/**
 * @param {string} word
 * @return {void}
 */
Trie.prototype.insert = function (word) {
  let temp = this;
  for (let i = 0; i < word.length; i++) {
    const c = word[i];
    // 原来不存在才创建，否则会丢失原有的数据
    if (!temp.next.get(c)) {
      temp.next.set(c, new Trie());
    }
    temp = temp.next.get(c);
  }
  temp.end = true;
};

/**
 * @param {string} word
 * @return {boolean}
 */
Trie.prototype.search = function (word) {
  let temp = this;
  for (let c of word) {
    // 获取下一个节点
    const node = temp.next.get(c);
    // 如果没有则说明没有添加过
    if (!node) {
      return false;
    }
    temp = node;
  }
  // 如果end为true说明添加的是这个单词，否则只能说明以这个单词为前缀
  return temp.end;
};

/**
 * @param {string} prefix
 * @return {boolean}
 */
Trie.prototype.startsWith = function (prefix) {
  let temp = this;
  for (let c of prefix) {
    const node = temp.next.get(c);
    if (!node) {
      return false;
    }
    temp = node;
  }
  return true;
};

/**
 * Your Trie object will be instantiated and called as such:
 * var obj = new Trie()
 * obj.insert(word)
 * var param_2 = obj.search(word)
 * var param_3 = obj.startsWith(prefix)
 */

全排列

46. 全排列 - 力扣（LeetCode）

题目中限定了没有重复的元素，递归时无需特判。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function (nums) {
  const ans = [];
  function dfs(nums, k) {
    if (nums.length === k) {
      ans.push(nums.slice());
      return;
    }
    for (let i = k; i < nums.length; i++) {
      // 交换当前位置和第i个位置的元素
      [nums[i], nums[k]] = [nums[k], nums[i]];
      dfs(nums, k + 1);
      // 复位
      [nums[i], nums[k]] = [nums[k], nums[i]];
    }
  }
  dfs(nums, 0);
  return ans;
};

子集

78. 子集 - 力扣（LeetCode）

求子集，核心思想可以用二进制考虑，每一个元素都有“要”或者“不要”两种选择，可以采用递归的方式，也可以采用迭代使用二进制方式，二进制的某位为 1 时表示要，0 表示不要。

使用回溯方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsets = function (nums) {
  const ans = [];
  function dfs(k, ret) {
    if (k === nums.length) {
      ans.push(ret.slice());
      return;
    }
    dfs(k + 1, ret);
    ret.push(nums[k]);
    dfs(k + 1, ret);
    // 归位，
    ret.pop();
  }
  dfs(0, []);
  return ans;
};

使用二进制方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsets = function (nums) {
  const ans = [];
  for (let i = 0; i < 1 << nums.length; i++) {
    const ret = [];
    for (let j = 0; j < nums.length; j++) {
      if (i & (1 << j)) {
        ret.push(nums[j]);
      }
    }
    ans.push(ret);
  }
  return ans;
};

电话号码的字母组合

17. 电话号码的字母组合 - 力扣（LeetCode）

也是一种组合问题，但是较为简单，给定一个一组数字字符串，按照这个顺序打出来的字母组合有哪些，因为数字顺序时固定的，可以每次从当前数字中挑一个对应的字母添加到结果末尾，然后选择下一个数字的字母，依次类推。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * @param {string} digits
 * @return {string[]}
 */
var letterCombinations = function (digits) {
  if (digits.length === 0) {
    return [];
  }
  const numDigit = {
    2: ['a', 'b', 'c'],
    3: ['d', 'e', 'f'],
    4: ['g', 'h', 'i'],
    5: ['j', 'k', 'l'],
    6: ['m', 'n', 'o'],
    7: ['p', 'q', 'r', 's'],
    8: ['t', 'u', 'v'],
    9: ['w', 'x', 'y', 'z'],
  };
  const ans = [];
  function dfs(k, ret) {
    if (k === digits.length) {
      ans.push(ret);
      return;
    }
    for (let c of numDigit[digits[k]]) {
      dfs(k + 1, ret.concat(c));
    }
  }
  dfs(0, '');
  return ans;
};

组合总和

39. 组合总和 - 力扣（LeetCode）

难点在于结果集不能重复，如[2, 2, 3]和[2, 3, 2]是重复的。因此在 dfs 时需要主动避免产生重复的结果。做法：每次搜索时设置下一次搜索的起点，避免后续的搜索会搜索前边搜索过的结果。

具体可参考：39. 组合总和 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function (candidates, target) {
  const ans = [];
  // idx表示这一轮搜索的起始位置
  function dfs(ret, sum, idx) {
    if (idx === candidates.length) {
      return;
    }
    if (sum === target) {
      ans.push(ret.slice());
      return;
    }
    // 此轮搜索不要当前值，则下一轮搜索需要从下一个位置开始
    dfs(ret, sum, idx + 1);
    if (sum + candidates[idx] <= target) {
      ret.push(candidates[idx]);
      // 此轮搜索要当前值，下一轮搜索也从当前位置开始
      dfs(ret, sum + candidates[idx], idx);
      ret.pop();
    }
  }
  dfs([], 0, 0);
  return ans;
};

括号生成

22. 括号生成 - 力扣（LeetCode）

多种方法可以做，这里先采取回溯法做。

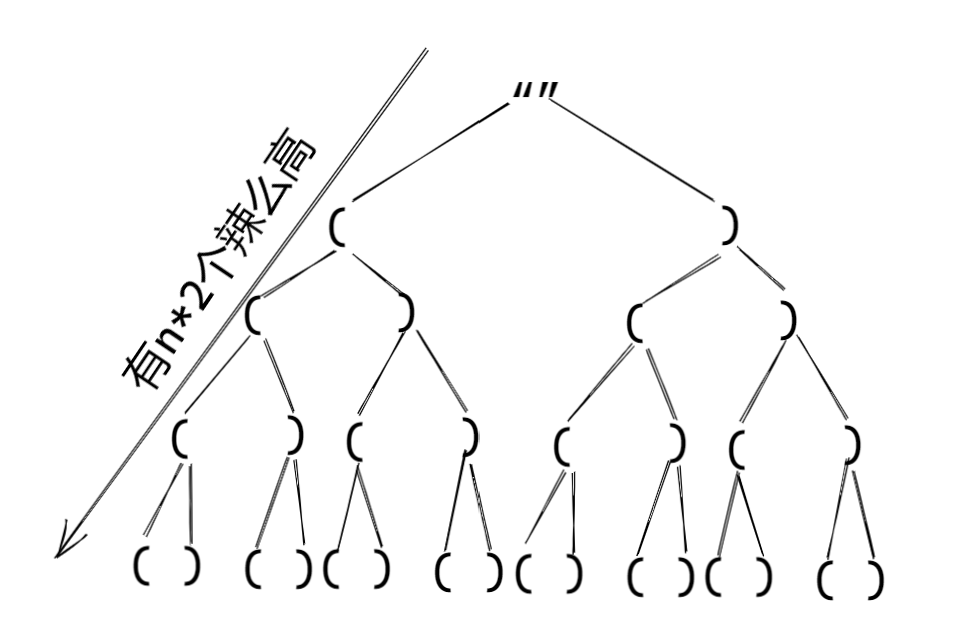
回溯的前提是使用深度优先搜索，然后使用剪枝策略优化。因此首先想到使用深搜搜索出所有的结果。画出递归树：

通过递归树可以看到，有些结果是不能要的，比如((((、))))等等，因此，在进行深搜时需要加上判断条件进行剪枝。

如果括号能匹配，首先左括号的个数不能超过n，因为这里是从前往后追加括号，因此左括号的个数优先增大，而且，如果想要后续的右括号可以匹配上左括号，左括号的个数一定要大于或等于右括号，否则像(()))，后续无论怎么追加括号，都不是合法的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * @param {number} n
 * @return {string[]}
 */
var generateParenthesis = function (n) {
  const ans = [];
  const path = [];
  function dfs(left, right) {
    if (left > n || left < right) {
      return;
    }
    if (path.length === 2 * n) {
      ans.push(path.join(''));
      return;
    }
    path.push('(');
    dfs(left + 1, right);
    path.pop();

    path.push(')');
    dfs(left, right + 1);
    path.pop();
  }
  dfs(0, 0);
  return ans;
};

单词搜索

79. 单词搜索 - 力扣（LeetCode）

此题需要用回溯才能达到最佳，因此要考虑剪枝策略。

首先按照深搜的方式，从某个点出发，遍历所有方向所有长度的字符串，直到找到符合条件的。

可以想到一个剪枝策略，当下一个字符和要查找的字符串的下一个字符匹配时才进行搜索，如果不匹配，即使搜索了，也是不满足的。

还有一个注意点，停止条件是：遍历到word字符串的最后一个位置时就要终止递归了。

因为dfs(i, j, idx)表示的是：board[i, j]位置的字符和word[idx]位置的字符相同，只有当相同的时候才会走进这个递归。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
var exist = function (board, word) {
  const m = board.length,
    n = board[0].length;
  const visited = new Array(m).fill(null).map((item) => new Array(n).fill(false));
  const dx = [0, 1, 0, -1],
    dy = [1, 0, -1, 0];
  let ans = false;
  function dfs(x, y, idx) {
    if (idx === word.length - 1) {
      ans = true;
      return;
    }
    if (ans) {
      return;
    }
    visited[x][y] = true;
    for (let i = 0; i < 4; i++) {
      const nx = x + dx[i],
        ny = y + dy[i];
      if (
        nx >= 0 &&
        nx < m &&
        ny >= 0 &&
        ny < n &&
        !visited[nx][ny] &&
        board[nx][ny] == word[idx + 1]
      ) {
        visited[nx][ny] = true;
        dfs(nx, ny, idx + 1);
        visited[nx][ny] = false;
      }
    }
    visited[x][y] = false;
  }
  for (let i = 0; i < board.length; i++) {
    for (let j = 0; j < board[i].length; j++) {
      board[i][j] === word[0] && dfs(i, j, 0);
    }
  }
  return ans;
};

分割回文串

131. 分割回文串 - 力扣（LeetCode）

用到了两种算法，一种是动态规划，一种是回溯。

回溯用于搜索到所有可能的子串，然后通过动态规划判断是否可以组成回文串。

使用一个下标i表示当前搜索到的位置，[0, i - 1]表示已经搜索过的，[i, n]表示没有搜索的，然后对[i, j]进行判断，如果可以构成回文串，则从j + 1开始进行下一次搜索。

动态规划主要用于快速判断是否是回文串，这里采用记忆化搜索的方式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * @param {string} s
 * @return {string[][]}
 */
var partition = function (s) {
  const ans = [];
  const f = new Array(s.length).fill(null).map((item) => new Array(s.length).fill(null));
  function dfs(i, ret) {
    if (i === s.length) {
      ans.push(ret.slice());
      return;
    }
    for (let j = i; j < s.length; j++) {
      if (dp(i, j)) {
        ret.push(s.slice(i, j + 1));
        dfs(j + 1, ret);
        ret.pop();
      }
    }
  }
  // 记忆化搜索的方式
  function dp(x, y) {
    if (f[x][y] !== null) {
      return f[x][y];
    }
    for (let i = x, j = y; i < j; i++, j--) {
      if (s[i] !== s[j]) {
        f[x][y] = false;
        return false;
      }
    }
    f[x][y] = true;
    return true;
  }
  dfs(0, []);
  return ans;
};

N 皇后

51. N 皇后 - 力扣（LeetCode）

难点在于怎么快速判断当前位置是否是可放的位置，即判断当前位置的行、列和两个对角线是否有其他皇后。

其中表示两个对角线是最难的。

可以将行和列看作是坐标系，将对角线平移的时候，和y轴的交点即为在数组中的下标，需要注意的是另一种情况下标会出现负数，因此可以将整体加上n - 1保证为正数，或者也可以使用哈希表存储不用考虑正负问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * @param {number} n
 * @return {string[][]}
 */
var solveNQueens = function (n) {
  const row = new Array(n).fill(false),
    col = row.slice();
  const diag = new Array(2 * n - 1),
    rediag = diag.slice();
  const ans = [];
  const place = new Array(n).fill(null).map((item) => new Array(n).fill('.'));
  function dfs(idx) {
    if (idx === n) {
      ans.push(place.map((item) => item.join('')));
      return;
    }
    for (let i = 0; i < n; i++) {
      if (check(idx, i)) {
        row[idx] = col[i] = diag[idx + i] = rediag[idx - i + n - 1] = true;
        place[idx][i] = 'Q';
        dfs(idx + 1);
        place[idx][i] = '.';
        row[idx] = col[i] = diag[idx + i] = rediag[idx - i + n - 1] = false;
      }
    }
  }
  function check(idx, i) {
    return !(row[idx] || col[i] || diag[idx + i] || rediag[idx - i + n - 1]);
  }
  dfs(0);
  return ans;
};

搜索插入位置

35. 搜索插入位置 - 力扣（LeetCode）

二分查找的题，记住这个二分经典模板即可。

二分经典模板即可解决这道题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var searchInsert = function (nums, target) {
  let left = 0,
    right = nums.length - 1;
  while (left <= right) {
    const mid = (left + right) >> 1;
    if (nums[mid] === target) {
      return mid;
    }
    if (nums[mid] > target) {
      right = mid - 1;
    } else {
      left = mid + 1;
    }
  }
  return left;
};

搜索二维矩阵

74. 搜索二维矩阵 - 力扣（LeetCode）

二维矩阵的搜索，从二分角度考虑，要寻找中间值，从题目中的排序规律可以看到，右上角的值处于中间位置，向左减小，向下增大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
  let x = 0,
    y = matrix[0].length - 1;
  while (x < matrix.length && y >= 0) {
    if (matrix[x][y] === target) {
      return true;
    } else if (matrix[x][y] > target) {
      y--;
    } else {
      x++;
    }
  }
  return false;
};

排序数组中查找第一个和最后一个位置

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

模板返回大于等于某个值的最小下标、小于等于某个值的最大下标。

结果需要注意特殊情况，如果大于等于的时候，当返回的结果是nums.length时，表示数组为空或者所有的值都小于target。如果小于等于的时候，返回的结果是-1时，表示数组为空或者所有的值都大于target。

当大于等于的时候最终的left为结果，小于等于的时候最终的right为结果。

只记住大于等于的模板即可，反过来的可以类比一下推出来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
var searchRange = function (nums, target) {
  function biSearch(nums, target, type) {
    let left = 0,
      right = nums.length - 1;
    // 注意这里是left <= right
    while (left <= right) {
      const mid = (left + right) >> 1;
      if (type === 0) {
        if (nums[mid] >= target) {
          right = mid - 1;
        } else {
          left = mid + 1;
        }
      } else {
        if (nums[mid] <= target) {
          left = mid + 1;
        } else {
          right = mid - 1;
        }
      }
    }
    return type === 0 ? left : right;
  }

  const start = biSearch(nums, target, 0);
  // 注意特殊情况处理。
  if (start === nums.length || nums[start] !== target) {
    return [-1, -1];
  }
  const end = biSearch(nums, target, 1);
  return [start, end];
};

搜索旋转排序数组

33. 搜索旋转排序数组 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function (nums, target) {
  if (nums.length === 0) {
    return -1;
  }
  let left = 0,
    right = nums.length - 1;
  // 注意是left <= right
  while (left <= right) {
    const mid = (left + right) >> 1;
    if (nums[mid] === target) {
      return mid;
    }
    // [left, mid]区间部分为非降序的
    if (nums[left] <= nums[mid]) {
      // 这里判断target在[left, mid)这个区间中，右开因为上一步判断了不相等
      // 左开因为target和nums[left]可能相等，
      if (nums[left] <= target && target < nums[mid]) {
        right = mid - 1;
      } else {
        left = mid + 1;
      }
      // [mid, right]区间部分为非降序的
    } else {
      if (nums[mid] < target && target <= nums[right]) {
        left = mid + 1;
      } else {
        right = mid - 1;
      }
    }
  }
  return -1;
};

寻找旋转排序数组中的最小值

153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

题目中给定的数组和上一题一样，依然是使用二分，这里和最后一个值进行比较，因为旋转后的最后一个值，是第二段区间的最大值，第一段区间的最小值。

注意返回的是**left**，可以按照“返回没有等号的那个被赋值的变量”，如**nums[mid] > nums[nums.length - 1]**条件中没有**=**，则返回**left**。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * @param {number[]} nums
 * @return {number}
 */
var findMin = function (nums) {
  let left = 0,
    right = nums.length - 1;
  while (left <= right) {
    const mid = (left + right) >> 1;
    if (nums[mid] > nums[nums.length - 1]) {
      left = mid + 1;
    } else {
      right = mid - 1;
    }
  }
  return nums[left];
};

寻找两个正序数组的中位数

4. 寻找两个正序数组的中位数 - 力扣（LeetCode）

要求O(log(m + 1))的复杂度，可以将问题转化为，两个正序数组中，寻找第k小的数，最多寻找两次即可寻找到两个中位数的位置。

具体可参考题解：4. 寻找两个正序数组的中位数 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
var findMedianSortedArrays = function (nums1, nums2) {
  const sumLen = nums1.length + nums2.length;
  function findKthSmallest(nums1, start1, end1, nums2, start2, end2, k) {
    const len1 = end1 - start1 + 1,
      len2 = end2 - start2 + 1;
    if (len1 > len2) return findKthSmallest(nums2, start2, end2, nums1, start1, end1, k);
    if (len1 === 0) return nums2[start2 + k - 1];
    if (k === 1) return Math.min(nums1[start1], nums2[start2]);
    const i = start1 + Math.min(Math.floor(k / 2), len1) - 1;
    const j = start2 + Math.min(Math.floor(k / 2), len2) - 1;
    if (nums1[i] < nums2[j]) {
      return findKthSmallest(
        nums1,
        i + 1,
        end1,
        nums2,
        start2,
        end2,
        k - (i - start1 + 1)
      );
    } else {
      return findKthSmallest(
        nums1,
        start1,
        end1,
        nums2,
        j + 1,
        end2,
        k - (j - start2 + 1)
      );
    }
  }
  if (sumLen % 2 === 0) {
    return (
      (findKthSmallest(
        nums1,
        0,
        nums1.length - 1,
        nums2,
        0,
        nums2.length - 1,
        Math.ceil(sumLen / 2)
      ) +
        findKthSmallest(
          nums1,
          0,
          nums1.length - 1,
          nums2,
          0,
          nums2.length - 1,
          Math.ceil(sumLen / 2) + 1
        )) /
      2
    );
  } else {
    return findKthSmallest(
      nums1,
      0,
      nums1.length - 1,
      nums2,
      0,
      nums2.length - 1,
      Math.ceil(sumLen / 2)
    );
  }
};

最小栈

155. 最小栈 - 力扣（LeetCode）

方法一：使用辅助栈

每次入栈时，使用另一个栈保存当前栈里的最小值，同步出入栈，会有额外的空间。

🍕 方法二：不适用额外空间，栈里保存的是每次入栈的值和最小值的差。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
var MinStack = function () {
  this.stk = [];
  this.minValue = -Infinity;
};

/**
 * @param {number} val
 * @return {void}
 */
MinStack.prototype.push = function (val) {
  // 初始没有数据，直接插入
  if (!this.stk.length) {
    this.stk.push(0);
    this.minValue = val;
  }
  // 有数据后，首先取差值diff，然后栈里插入diff
  // 如果diff为正，则说明插入值大，最小值不变，否则说明有更小的，更新最小值
  else {
    const diff = val - this.minValue;
    this.stk.push(diff);
    this.minValue = diff > 0 ? this.minValue : val;
  }
};

/**
 * @return {void}
 */
MinStack.prototype.pop = function () {
  if (this.stk.length) {
    const diff = this.stk.pop();
    // 如果差值大于0，说明插入这一个数时，没有更新最小值，由于diff = val - minValue
    // 所以反推出val = diff + minValue
    if (diff > 0) {
      const top = diff + this.minValue;
    }
    // 如果不大于0，说明插入时更新了最小值，最小值即为真实值，所以直接取最小值
    // 因为最小值更新了，所以更新回来，diff = val - minValue反推
    else {
      const top = this.minValue;
      this.minValue = top - diff;
    }
  }
};

/**
 * @return {number}
 */
MinStack.prototype.top = function () {
  // 同理
  if (this.stk.length) {
    const diff = this.stk.at(-1);
    return diff > 0 ? diff + this.minValue : this.minValue;
  }
};

/**
 * @return {number}
 */
MinStack.prototype.getMin = function () {
  return this.minValue;
};

/**
 * Your MinStack object will be instantiated and called as such:
 * var obj = new MinStack()
 * obj.push(val)
 * obj.pop()
 * var param_3 = obj.top()
 * var param_4 = obj.getMin()
 */

字符串解码

394. 字符串解码 - 力扣（LeetCode）

方法 1

根据规则，可以看作是一个递归的过程，递归调用。

用栈是为了匹配括号，首先匹配到最外层的括号，然后对括号内的字符串进行递归调用解码。

需要注意：数字和括号的前后都可能存在不需要解码的字符串，仍然需要拼接到结果中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * @param {string} s
 * @return {string}
 */
var decodeString = function (s) {
  let ans = '';
  const stk = [];
  // 记录需要解码的字符串的其实位置，主要用于拼接前半部分不用解码的字符串
  let start = 0;
  for (let i = 0; i < s.length; i++) {
    if (s[i] === '[') {
      stk.push(i);
    } else if (s[i] === ']') {
      if (stk.length === 1) {
        const idx = stk.pop();
        let j = idx - 1;
        while (j >= 0 && '0' <= s[j] && s[j] <= '9') j--;
        j++;
        const cnt = Number(s.slice(j, idx));
        ans = ans
          .concat(s.slice(start, j))
          .concat(decodeString(s.slice(idx + 1, i)).repeat(cnt));
        start = i + 1;
      } else {
        stk.pop();
      }
    }
  }
  // 如果没有到最后s.length，说明最后的字符串为不用解码的
  if (start !== s.length) {
    ans = ans.concat(s.slice(start));
  }
  return ans || s;
};

方法 2

按顺序依次遍历，栈中存储要循环的次数以及当前循环之前的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
var decodeString = function (s) {
  const arr = [...s];
  let ans = [];
  const stk = [];
  let cnt = 0;
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] <= '9' && arr[i] >= '0') {
      cnt = cnt * 10 + Number(arr[i]);
    } else if (arr[i] === '[') {
      stk.push([cnt, ans.slice()]);
      cnt = 0;
      ans = [];
    } else if (arr[i] === ']') {
      const [multi, ret] = stk.pop();
      ret.push(...[...ans.join('').repeat(multi)]);
      ans = ret;
    } else {
      ans.push(arr[i]);
    }
  }
  return ans.join('');
};

每日温度

739. 每日温度 - 力扣（LeetCode）

使用单调栈，栈底到栈顶元素依次递减。只要元素在栈中，就说明目前没有发现后续有比该元素大的。

栈里存储的是元素下标，方便计算差了多少天。

如果栈空，直接入栈

否则，如果元素比栈顶元素大，说明栈顶元素后的第一个大的就是当前元素，取出来，计算差值。

否则，跳过直接加入到栈中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * @param {number[]} temperatures
 * @return {number[]}
 */
var dailyTemperatures = function (temperatures) {
  const stk = [],
    ans = new Array(temperatures.length).fill(0);
  for (let i = 0; i < temperatures.length; i++) {
    while (stk.length && temperatures[stk.at(-1)] < temperatures[i]) {
      const t = stk.pop();
      ans[t] = i - t;
    }
    stk.push(i);
  }
  return ans;
};

数组中第 K 个最大的元素

215. 数组中的第 K 个最大元素 - 力扣（LeetCode）

要求用O(n)的复杂度，数学证明快速选择算法为O(n)复杂度，因此直接使用即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var findKthLargest = function (nums, k) {
  function quickChoice(nums, left, right, k) {
    if (left >= right) return nums[left];
    let less = left - 1,
      i = left,
      more = right + 1;
    const x = nums[Math.floor((left + right) / 2)];
    while (i < more) {
      if (nums[i] < x) {
        less++;
        [nums[i], nums[less]] = [nums[less], nums[i]];
        i++;
      } else if (nums[i] > x) {
        more--;
        [nums[i], nums[more]] = [nums[more], nums[i]];
      } else {
        i++;
      }
    }
    if (less < k && k < more) return nums[k];
    if (k <= less) return quickChoice(nums, left, less, k);
    if (k >= more) return quickChoice(nums, more, right, k);
  }
  return quickChoice(nums, 0, nums.length - 1, nums.length - k);
};

前 K 个高频元素

347. 前 K 个高频元素 - 力扣（LeetCode）

题目要求复杂度优于O(nlogn)，前 K 个元素很容易联想到堆这种数据结构。

要求频率大小，首先可以遍历数组求出每个元素出现的次数，然后用大小为K 的小根堆存储次数，使用小根堆原因是：如果新元素大于堆顶，说明在已知的前 K 个元素中，新元素能把堆顶元素踢掉（堆顶肯定不是前 K 个了），剩余的元素都大于堆顶。直到遍历完所有的频率次数组合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var topKFrequent = function (nums, k) {
  const numCnt = new Map();
  for (const num of nums) {
    if (numCnt.has(num)) {
      numCnt.set(num, numCnt.get(num) + 1);
    } else {
      numCnt.set(num, 1);
    }
  }
  const heap = [];
  // 比较函数，返回负数时，parent在son前边，为0时，顺序不变，正数时parent在son后边
  const fn = (parent, son) => {
    return parent.cnt - son.cnt;
  };
  for (const [num, cnt] of numCnt) {
    if (heap.length < k) {
      heap.push({ num, cnt });
      heapUp(heap, heap.length - 1, fn);
    } else if (heap[0].cnt < cnt) {
      heap[0] = { num, cnt };
      heapDown(heap, 0, k, fn);
    }
  }
  return heap.map((item) => item.num);
};

function heapUp(arr, idx, fn) {
  let parentIdx;
  // 比较函数结果为正数时才交换
  while (fn(arr[(parentIdx = Math.trunc((idx - 1) / 2))], arr[idx]) > 0) {
    swap(arr, parentIdx, idx);
    idx = parentIdx;
  }
}

function heapDown(arr, idx, size, fn) {
  let t = idx,
    left = 2 * idx + 1,
    right = 2 * idx + 2;
  if (left < size && fn(arr[t], arr[left]) > 0) {
    t = left;
  }
  if (right < size && fn(arr[t], arr[right]) > 0) {
    t = right;
  }
  if (t !== idx) {
    swap(arr, t, idx);
    heapDown(arr, t, size, fn);
  }
}

function swap(arr, i, j) {
  const t = arr[i];
  arr[i] = arr[j];
  arr[j] = t;
}

跳跃游戏

55. 跳跃游戏 - 力扣（LeetCode）

贪心算法，如果能到达i，那么从i位置能到达的最远的位置是i + nums[i]，记为maxDistance，然后继续向后计算，如果i + 1 <= maxDistance，就说明在上一步的前提下，可以到达i + 1位置，然后基于该位置更新maxDistance。初始时最远位置是 0。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    bool canJump(vector<int>& nums) {
        int maxDistance = 0;
        for (int i = 0; i < nums.size(); i++) {
            if (i <= maxDistance) {
                maxDistance = max(maxDistance, i + nums[i]);
            }
        }
        return maxDistance >= nums.size() - 1;
    }
};

跳跃游戏 Ⅱ

45. 跳跃游戏 II - 力扣（LeetCode）

贪心算法，题目中保证一定可以到最终位置。在位置i时，可以到达的最远位置为i + nums[i]，那么是不是应该跳到i + nums[i]位置呢？不一定。从i位置最远可以跳到i + nums[i]，如果j位置(i <= j <= i + nums[i])，并且从j位置跳的最远距离在这个区间中时最远的，那么下一步应该跳到j位置，保证下一步跳的最远。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int jump(vector<int>& nums) {
        int maxPos = 0, ans = 0, i = 0;
        while (maxPos < nums.size() - 1) {
            int end = 0;
            for (int j = i; j <= maxPos; j++) {
                end = max(end, j + nums[j]);
            }
            i = maxPos;
            maxPos = end;
            ans++;
        }
        return ans;
    }
};

完全平方数

279. 完全平方数 - 力扣（LeetCode）

动态规划，f[i]表示i这个数的完全平方数的最少数量。

由定义可知，组成i这个数的完全平方数的范围肯定在image之间，因此可以遍历一遍，设j在这个区间内，那么如果完全平方数包含j这个数，剩余的数的最少数量则由f[i - j * j]表示，可以看成子问题，使用动态规划做。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * @param {number} n
 * @return {number}
 */
var numSquares = function (n) {
  const f = new Array(n + 1).fill(Infinity);
  f[0] = 0;
  for (let i = 1; i < f.length; i++) {
    for (let j = 1; j <= i / j; j++) {
      f[i] = Math.min(f[i], f[i - j * j] + 1);
    }
  }
  return f.at(-1);
};

零钱兑换

322. 零钱兑换 - 力扣（LeetCode）

思路同上

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * @param {number[]} coins
 * @param {number} amount
 * @return {number}
 */
var coinChange = function (coins, amount) {
  const f = new Array(amount + 1).fill(Infinity);
  f[0] = 0;
  for (let i = 1; i < f.length; i++) {
    for (const coin of coins) {
      if (i >= coin) {
        f[i] = Math.min(f[i], f[i - coin] + 1);
      }
    }
  }
  return f.at(-1) === Infinity ? -1 : f.at(-1);
};

单词拆分

139. 单词拆分 - 力扣（LeetCode）

动态规划，f[i]表示以前i个字符串能否被表示出来，遍历单词字典，如果前i个字符串的最后的word.size()长度的子字符串和word相等，则说明可以通过word组成，再判断f[i - word.size()]能否组成即可，子问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * @param {string} s
 * @param {string[]} wordDict
 * @return {boolean}
 */
var wordBreak = function (s, wordDict) {
  const f = new Array(s.length + 1).fill(false);
  f[0] = true;
  for (let i = 1; i <= s.length; i++) {
    for (const word of wordDict) {
      if (word.length > i) continue;
      if (s.slice(i - word.length, i) === word) {
        f[i] = f[i - word.length];
      }
      if (f[i]) break;
    }
  }
  return f.at(-1);
};

最长递增子序列

300. 最长递增子序列 - 力扣（LeetCode）

要求O(nlogn)的复杂度，考虑二分查找。

状态定义：f[i]表示长度为i的递增子序列的最后一个元素所有可能的取值的最小值。

根据定义，猜想：f数组是递增的。

反证法：如果f[k] >= f[i]且k = i - 1，那么在以f[i]结尾的子序列中，倒数第二个元素（记为v）一定小于f[i]，以v为结尾的子序列长度为k。因为f[i] > v且f[k] >= f[i]所以f[k] > v，与f的定义矛盾。因为长度为k的子序列的最后一个元素是所有可能取值里最小的，初始条件取的f[k]但是推出的结论v < f[k]，说明f[k]不是最小，矛盾。

每遍历一个数，从f中求小于num的最大的位置（也就是大于等于num的最小的位置）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        // f[i] 表示递增子序列长度为 i 时的子序列的最后一个元素的可能的最小值
        vector<int> f(nums.size() + 1, 0);
        int len = 0;
        for (int i = 0; i < nums.size(); i++) {
            int left = 1, right = len;
            while (left <= right) {
                int mid = left + right >> 1;
                // 注意这里二分的含义是 大于等于 nums[i] 的最小的，不能理解为 小于 nums[i] 的最大的
                // 如果找得到则 left 正好是对应的位置，如果找不到，即所有的数都小于 nums[i] ，则结果为 右边界 + 1
                if (f[mid] >= nums[i]) right = mid - 1;
                else left = mid + 1;
            }
            len = max(len, left);
            f[left] = nums[i];
        }
        return len;
    }
};

乘积最大子数组

152. 乘积最大子数组 - 力扣（LeetCode）

动态规划，f[i]表示以nums[i]为结尾的子数组的最大乘积，但是这样会出现问题，因为每个元素可能会出现负值，如果是负值，那么期望前一个子数组的乘积越小越好，这与最初定义相反。因此可以维护另一个数组，存储子数组的最小乘积。

maxF[i]表示子数组最大乘积，minF[i]表示子数组最小乘积。

每次遍历时最大值从maxF[i - 1] * nums[i], minF[i - 1] * nums[i], nums[i]中取，最小值同理。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maxProduct(vector<int>& nums) {
        vector<int> maxF(nums.size(), 0);
        vector<int> minF(nums.size(), 0);
        maxF[0] = minF[0] = nums[0];
        for (int i = 1; i < nums.size(); i++) {
            maxF[i] = max(max(maxF[i - 1] * nums[i], minF[i - 1] * nums[i]), nums[i]);
            minF[i] = min(min(minF[i - 1] * nums[i], maxF[i - 1] * nums[i]), nums[i]);
        }
        return *max_element(maxF.begin(), maxF.end());
    }
};

分割等和子集

416. 分割等和子集 - 力扣（LeetCode）

可以改造成背包问题，分成两个子集，两个子集的和相等，转化为找一个子集的和恰好为整个数组的和的一半，即选取一些数，这些数的和恰好等于总和的一半。

和原背包不同的是原背包是小于体积，这个问题是恰好等于“体积”。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for (int num : nums) sum += num;
        if (sum % 2 != 0) return false;
        // f[i][j] 表示拿前 i 个物品（数）的累加和是否恰好等于 j
        vector<vector<bool>> f(nums.size() + 1, vector<bool>(sum / 2 + 1, false));
        for (int i = 0; i < f[0].size(); i++) f[0][i] = false;
        for (int i = 0; i < f.size(); i++) f[i][0] = true;
        for (int j = 1; j < f[0].size(); j++) {
            for (int i = 1; i < f.size(); i++) {
                // 如果当前要取的数小于或等于“体积”，可以选择拿或者不拿
                // 如果不拿，则是否恰好等于 j 取决于前 i - 1 个数的条件
                // 如果拿，则取决于前 i - 1 个数体积为 j - nums[i - 1] 的条件，因为要保证拿了这个数恰好等于 j，所以要减去 nums[i - 1]
                if (nums[i - 1] <= j) f[i][j] = f[i - 1][j] || f[i - 1][j - nums[i - 1]];
                // 如果大于，则肯定拿不了
                else f[i][j] = f[i - 1][j];
            }
        }
        return f.back().back();
    }
};

最长回文子串

5. 最长回文子串 - 力扣（LeetCode）

如果字符串长度为 1，则肯定是回文串，直接返回，如果字符串长度为 2，则判断两个字符是否相等，如果相等，则返回，否则最长回文子串就是一个字符。

其余情况：

使用f[i][j]表示子串s[i]...s[j]是否是回文子串，是不是回文子串取决于s[i] s[j]是不是相等，如果不相等，则肯定不是回文的，否则判断f[i + 1][j - 1]是不是回文的。

如果f[i + 1][j - 1]是回文的，则f[i][j]是不是回文取决于在前后追加的字符是否相同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    string longestPalindrome(string s) {
        const int n = s.size();
        if (n == 1) return s;
        if (n == 2) return s[0] == s[1] ? s : string(1, s[0]);
        vector<vector<bool>> f(n, vector<bool>(n, false));
        // 初始化长度为 1 和为 2 的情况
        for (int i = 0; i < n; i++) {
            f[i][i] = true;
            if (i > 0) f[i - 1][i] = s[i - 1] == s[i];
        }
        // 从长度为 3 开始遍历
        for (int len = 3; len <= n; len++) {
            for (int i = 0; i + len - 1 < n; i++) {
                int j = i + len - 1;
                f[i][j] = f[i + 1][j - 1] && s[i] == s[j];
            }
        }
        int maxLen = 1;
        int x = 0, y = 0;
        for (int i = 0; i < n; i++) {
            for (int j = i; j < n; j++) {
                if (f[i][j] && maxLen < j - i + 1) {
                    maxLen = j - i + 1;
                    x = i, y = j;
                }
            }
        }
        return s.substr(x, maxLen);
    }
};

下一个排列

31. 下一个排列 - 力扣（LeetCode）

按照字典序求下一个排列，题解：31. 下一个排列 - 力扣（LeetCode）

流程：

  1. 从后往前找第一个相邻的升序对 (i, j)
  2. 在 [j, end) 这个区间中从后向前寻找第一个比 nums[i]大的数nums[k]
  3. 交换 nums[i] nums[k]
  4. 再将 [j, end) 的区间逆序。

总体思路：

  • 将后边较大的数与前边较小的数交换，即可以让数值更大。
  • 因为是下一个排列，同时也希望增大的不是特别快。所以希望较大的数尽量的小。
  • 交换完后，后续的数肯定是降序，反转改成升序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        if (nums.size() <= 1) return;
        int i = nums.size() - 2, j = i + 1, k = j;
        for (; i >= 0; i--, j--) {
            if (nums[i] < nums[j]) break;
        }
        // 如果 i >= 0 说明不是最后一个排列，可以继续向下寻找，否则说明是最后一个排列，则直接跳过
        // 执行后续步骤就会回到第一个排列
        if (i >= 0) {
            for (; k >= j; k--) {
                if (nums[i] < nums[k]) break;
            }
            swap(nums[i], nums[k]);
        }
        for (int a = j, b = nums.size() - 1; a < b; a++, b--) {
            swap(nums[a], nums[b]);
        }
    }
};

寻找重复数

287. 寻找重复数 - 力扣（LeetCode）

看成链表的形式，如果存在重复的数，说明链表中存在环。链表有环判断，通过快慢指针。142. 环形链表 II - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int fast = 0, slow = 0;
        while (true) {
            fast = nums[nums[fast]];
            slow = nums[slow];
            if (fast == slow) {
                slow = 0;
                while (fast != slow) {
                    fast = nums[fast];
                    slow = nums[slow];
                }
                return slow;
            }
        }
        return 0;
    }
};

数据流中的中位数

295. 数据流的中位数 - 力扣（LeetCode）

要求低时间复杂度，根据中位数的定义，使用两个优先队列（堆）存储，一个保存中位数前半部分，一个保存后半部分，加入元素时，判断属于哪一部分，加入完毕后，判断两个队列长度是否相等或者后半部分长度多一个。否则将多的数加入到另一个队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class MedianFinder {
public:
    priority_queue<int, vector<int>, less<int>> largeHeap;
    priority_queue<int, vector<int>, greater<int>> smallHeap;
    MedianFinder() {

    }

    void addNum(int num) {
        if (smallHeap.empty() || num >= smallHeap.top()) {
            smallHeap.push(num);
            if (smallHeap.size() > largeHeap.size() + 1) {
                largeHeap.push(smallHeap.top());
                smallHeap.pop();
            }
        } else {
            largeHeap.push(num);
            if (largeHeap.size() > smallHeap.size()) {
                smallHeap.push(largeHeap.top());
                largeHeap.pop();
            }
        }
    }

    double findMedian() {
        if (smallHeap.size() == largeHeap.size())
            return 1.0 * (smallHeap.top() + largeHeap.top()) / 2;
        return smallHeap.top();
    }
};

柱状图中最大的矩形

84. 柱状图中最大的矩形 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        // 单调递增栈
        stack<int> st;
        // 分别保存第 i 个元素的左边、右边的最近的比 heights[i] 小的位置
        vector<int> left(n), right(n);
        for (int i = 0; i < n; i++) {
            while (!st.empty() && heights[i] <= heights[st.top()]) {
                st.pop();
            }
            // 如果栈空，说明左边的元素都比当前元素大，在之前的存在栈中的元素中当前元素最小
            // 直接设为 -1 （哨兵值，方便后期计算）
            left[i] = st.empty() ? -1 : st.top();
            st.push(i);
        }
        stack<int>().swap(st);
        for (int i = n - 1; i >= 0; i--) {
            while (!st.empty() && heights[i] <= heights[st.top()]) {
                st.pop();
            }
            right[i] = st.empty() ? n : st.top();
            st.push(i);
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
            // right[i] 和 left[i] 存储的是右边和左边的最近的最小的位置，按照
            // height[i] 高度寻找最大的矩形，left[i] 和 right[i] 位置的高度都无法参与构成
            // 因此要剔除这两个，所以需要多减一个 1
            ans = max(ans, (right[i] - left[i] - 1) * heights[i]);
        }
        return ans;
    }
};

最长有效括号

32. 最长有效括号 - 力扣（LeetCode）

f[i]表示以i位置为结尾的最长有效括号长度。

如果s[i] == '('则肯定不是有效括号

如果s[i] == ')'，则如果s[i - 1] == '('，最后两个元素可以构成有效括号，再加上f[i - 2]的长度即可。则如果s[i - 1] == ')'，判断s[i - f[i - 1] - 1] == '('（判断以s[i - 1]结尾的有效长度的上一个位置是否是左括号），相等的话，则说明[i - f[i - 1] - 1], i]的范围内，两边可以组成括号，中间内部能否组成由f[i - 1]决定，最后加上f[i - f[i - 1] - 2]的长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int longestValidParentheses(string s) {
        if (s.size() == 0) return 0;
        vector<int> f(s.size(), 0);
        for (int i = 0; i < s.size(); i++) {
            if (s[i] == '(') continue;
            if (i > 0 && s[i - 1] == '(') {
                f[i] = i > 1 ? f[i - 2] + 2 : 2;
            } else if (i > 0 && s[i - 1] == ')') {
                if (i - f[i - 1] - 1 >= 0 && s[i - f[i - 1] - 1] == '(') {
                    f[i] = f[i - 1] + (i - f[i - 1] - 2 >= 0 ? f[i - f[i - 1] - 2] : 0) + 2;
                }
            }
        }
        return *max_element(f.begin(), f.end());
    }
};
LeetCode Hot100
2023/12/01/LeetCode/LeetCodeHot100/
作者
yatbfm
发布于
2023-12-01 21:39
许可
  1. 盛最多水的容器
  2. 三数之和
  3. 最长连续序列
  4. 接雨水
  5. 无重复字符的最长子串
  6. 和为 K 的子数组
  7. 滑动窗口最大值
  8. 最小覆盖子串
  9. 最大子数组和
  10. 轮转数组
  11. 缺失的第一个正数
  12. 旋转图像
  13. 相交链表
  14. 反转链表
  15. 回文链表
  16. 环形链表
  17. 删除链表的倒数第 N 个节点
  18. 两两交换链表中的节点
  19. K 个一组翻转链表
  20. 随机链表的复制
  21. 排序链表
  22. 合并 K 个升序链表
  23. 实现 LRU 缓存
  24. 二叉树的层序遍历
  25. 将有序数组转为平衡二叉搜索树
  26. 验证是否是二叉搜索树
  27. 二叉搜索树第 K 小的元素
  28. 二叉树的右视图
  29. 二叉树展开为链表
  30. 从前序遍历和中序遍历构造二叉树
  31. 路径总和 Ⅲ
  32. 二叉树的最近公共祖先
  33. 二叉树中的最大路径和
  34. 岛屿数量
  35. 腐烂的橘子
  36. 课程表
  37. 实现 Trie 树
  38. 全排列
  39. 子集
  40. 电话号码的字母组合
  41. 组合总和
  42. 括号生成
  43. 单词搜索
  44. 分割回文串
  45. N 皇后
  46. 搜索插入位置
  47. 搜索二维矩阵
  48. 排序数组中查找第一个和最后一个位置
  49. 搜索旋转排序数组
  50. 寻找旋转排序数组中的最小值
  51. 寻找两个正序数组的中位数
  52. 最小栈
  53. 字符串解码
    1. 方法 1
    2. 方法 2
  54. 每日温度
  55. 数组中第 K 个最大的元素
  56. 前 K 个高频元素
  57. 跳跃游戏
  58. 跳跃游戏 Ⅱ
  59. 完全平方数
  60. 零钱兑换
  61. 单词拆分
  62. 最长递增子序列
  63. 乘积最大子数组
  64. 分割等和子集
  65. 最长回文子串
  66. 下一个排列
  67. 寻找重复数
  68. 数据流中的中位数
  69. 柱状图中最大的矩形
  70. 最长有效括号
© 2020 - 2025    yatbfm
由 Hexo 驱动 & 主题 Keep
访客数 访问量
  1. 盛最多水的容器
  2. 三数之和
  3. 最长连续序列
  4. 接雨水
  5. 无重复字符的最长子串
  6. 和为 K 的子数组
  7. 滑动窗口最大值
  8. 最小覆盖子串
  9. 最大子数组和
  10. 轮转数组
  11. 缺失的第一个正数
  12. 旋转图像
  13. 相交链表
  14. 反转链表
  15. 回文链表
  16. 环形链表
  17. 删除链表的倒数第 N 个节点
  18. 两两交换链表中的节点
  19. K 个一组翻转链表
  20. 随机链表的复制
  21. 排序链表
  22. 合并 K 个升序链表
  23. 实现 LRU 缓存
  24. 二叉树的层序遍历
  25. 将有序数组转为平衡二叉搜索树
  26. 验证是否是二叉搜索树
  27. 二叉搜索树第 K 小的元素
  28. 二叉树的右视图
  29. 二叉树展开为链表
  30. 从前序遍历和中序遍历构造二叉树
  31. 路径总和 Ⅲ
  32. 二叉树的最近公共祖先
  33. 二叉树中的最大路径和
  34. 岛屿数量
  35. 腐烂的橘子
  36. 课程表
  37. 实现 Trie 树
  38. 全排列
  39. 子集
  40. 电话号码的字母组合
  41. 组合总和
  42. 括号生成
  43. 单词搜索
  44. 分割回文串
  45. N 皇后
  46. 搜索插入位置
  47. 搜索二维矩阵
  48. 排序数组中查找第一个和最后一个位置
  49. 搜索旋转排序数组
  50. 寻找旋转排序数组中的最小值
  51. 寻找两个正序数组的中位数
  52. 最小栈
  53. 字符串解码
    1. 方法 1
    2. 方法 2
  54. 每日温度
  55. 数组中第 K 个最大的元素
  56. 前 K 个高频元素
  57. 跳跃游戏
  58. 跳跃游戏 Ⅱ
  59. 完全平方数
  60. 零钱兑换
  61. 单词拆分
  62. 最长递增子序列
  63. 乘积最大子数组
  64. 分割等和子集
  65. 最长回文子串
  66. 下一个排列
  67. 寻找重复数
  68. 数据流中的中位数
  69. 柱状图中最大的矩形
  70. 最长有效括号